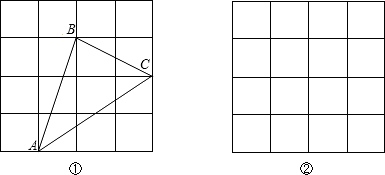
题目内容
正方形网格中，每个小正方形的边长为1．图1所示的矩形是由4个全等的直角梯形拼接而成的（图形的各顶点都在格点上；拼接时图形互不重叠，不留空隙），如果用这4个直角梯形拼接成一个等腰梯形，那么
（1）仿照图1，在图2中画出一个拼接成的等腰梯形；
（2）这个拼接成的等腰梯形的周长为 12+2
．
解：（1）
如图直角梯形AGHB、GHRQ、QRFE、EFCD组成等腰梯形ABCD．
（2）根据题意得到：AG=5，BC=7，AB=CD=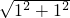
=，
∴等腰梯形的周长是5+7+2=12+2．
故答案为：12+2．
分析：（1）根据题意画出图形即可；
（2）求出AD、AB、CD、BC的长，即可求出答案．
点评：本题主要考查对等腰梯形的性质，直角梯形，勾股定理等知识点的理解和掌握，能正确画出图形是解此题的关键．
如图直角梯形AGHB、GHRQ、QRFE、EFCD组成等腰梯形ABCD．
（2）根据题意得到：AG=5，BC=7，AB=CD=
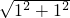=，∴等腰梯形的周长是5+7+2
=12+2．故答案为：12+2
．分析：（1）根据题意画出图形即可；
（2）求出AD、AB、CD、BC的长，即可求出答案．
点评：本题主要考查对等腰梯形的性质，直角梯形，勾股定理等知识点的理解和掌握，能正确画出图形是解此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12、如图是某学校的平面示意图，在10×10的正方形网格中（每个小方格都是边长为1的正方形），如果分别用（3，1），（3，5）表示图中图书馆和教学楼的位置，那么实验楼的位置应表示为
分析，探究回答下列问题：
