题目内容
如图,正方形网格中的每个小正方形边长都是1,每个小正方形的顶点叫格点,以格点为顶点的三角形称为格点三角形:(1)如图①,已知格点△ABC,分别求三边的长,并判断这个三角形是否直角三角形;
(2)画格点△DEF,使其为钝角三角形,且面积为4(在图②中画一个即可).
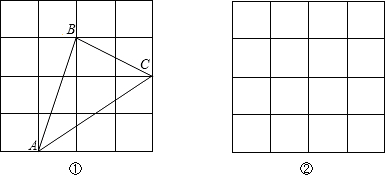
分析:(1)先根据勾股定理求出AB、BC及AC的长,再根据勾股定理的逆定理进行判断即可;
(2)根据题意画出钝角三角形,使三角形的面积为4即可.
(2)根据题意画出钝角三角形,使三角形的面积为4即可.
解答:解:(1)∵AB=
(1分),BC=
(2分)
AC=
,(3分),
∵AB2+BC2≠AC2(4分),
∴这个三角形不是直角三角形;(5分)
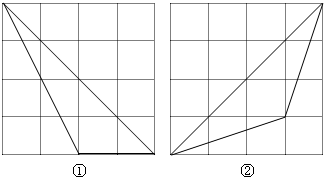
(2)如图所示.
| 10 |
| 5 |
AC=
| 13 |
∵AB2+BC2≠AC2(4分),
∴这个三角形不是直角三角形;(5分)
(2)如图所示.

点评:本题考查的是勾股定理及三角形的面积,熟知勾股定理及其逆定理、三角形的面积公式是解答此题的关键.

练习册系列答案
相关题目


 (1)先化简,再求值:x(x-2)-(x+1)(x-1),其中x=10.
(1)先化简,再求值:x(x-2)-(x+1)(x-1),其中x=10.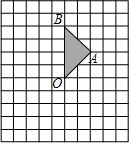 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABO的三个顶点A,B,O都在格点上.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABO的三个顶点A,B,O都在格点上.