题目内容
如图是在6×5的正方形网格中(每个小正方形的边长均为1),以格点为顶点的三角形称为网格三角形,请通过画图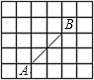 分析,探究回答下列问题:
分析,探究回答下列问题:(1)请在图中画出以AB为边且面积为2的一个网格三角形;
(2)任取该网格中的一点N,求以A、B、N为顶点的三角形面积为2的概率;
(3)任取该网格中的一点M,求以A、B、M为顶点的三角形中为等腰三角形的概率.
分析:(1)可以直接画出一个满足条件的三角形;
(2)首先找出可以组成的所有三角形的个数,然后再计算面积为2的三角形的个数,由此可得到所求的概率;
(3)首先找出可以组成的所有三角形的个数,然后再看其中的直角三角形的个数,由此可得到所求的概率.
(2)首先找出可以组成的所有三角形的个数,然后再计算面积为2的三角形的个数,由此可得到所求的概率;
(3)首先找出可以组成的所有三角形的个数,然后再看其中的直角三角形的个数,由此可得到所求的概率.
解答: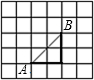 解:(1)如图所示(共9个,这是其中一个):
解:(1)如图所示(共9个,这是其中一个):
(2)由分析可知:只要N不在AB上或者AB的延长线上,A、B、N都可以构成三角形,共有6×7-6═36个,
又∵由(1)知,以A、B、M为顶点的三角形的面积为2的三角形共有9个,
∴P(以A、B、N为顶点的三角形面积为2)=
=
=
;
(3)∵以A、B、M为顶点的三角形中为等腰三角形共有8个,
∴P(以A、B、M为顶点的等腰三角形)=
=
=
.
 解:(1)如图所示(共9个,这是其中一个):
解:(1)如图所示(共9个,这是其中一个):(2)由分析可知:只要N不在AB上或者AB的延长线上,A、B、N都可以构成三角形,共有6×7-6═36个,
又∵由(1)知,以A、B、M为顶点的三角形的面积为2的三角形共有9个,
∴P(以A、B、N为顶点的三角形面积为2)=
| 9 |
| 6×7-6 |
| 9 |
| 36 |
| 1 |
| 4 |
(3)∵以A、B、M为顶点的三角形中为等腰三角形共有8个,
∴P(以A、B、M为顶点的等腰三角形)=
| 8 |
| 6×7-6 |
| 8 |
| 36 |
| 2 |
| 9 |
点评:本题主要考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
相关题目
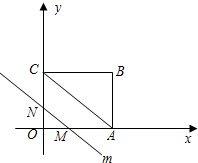 矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).
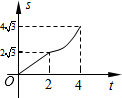
矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).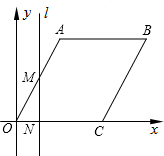 如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )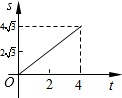
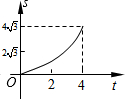
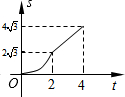
 转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒.
转90°,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒.
 ).
).