题目内容
【题目】科幻小说《实验室的故事》中,有这样一个情节:科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表).

由这些数据,科学家推测出植物每天高度增长量y是温度x的函数.且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度x应该在哪个范围内选择?请直接写出结果.
【答案】(1)选择二次函数,![]() ,理由见解析;(2)-1℃;(3)-6℃<x<4℃.
,理由见解析;(2)-1℃;(3)-6℃<x<4℃.
【解析】
(1)选择二次函数,设![]() (
(![]() ),然后选择
),然后选择![]() 、
、![]() 、
、![]() 三组数据,利用待定系数法求二次函数解析式即可,再根据反比例函数的自变量
三组数据,利用待定系数法求二次函数解析式即可,再根据反比例函数的自变量![]() 不能为
不能为![]() ,一次函数的特点,即可排除另两种函数;
,一次函数的特点,即可排除另两种函数;
(2)把二次函数解析式整理成顶点式形式,再根据二次函数的最值问题解答;
(3)求出平均每天的高度增长量为![]() ,然后根据
,然后根据![]() 求出
求出![]() 的值,再根据二次函数的性质写出
的值,再根据二次函数的性质写出![]() 的取值范围.
的取值范围.
(1)选择二次函数,设![]() (
(![]() ),
),
∵![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() ,
,
∴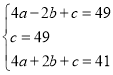 ,
,
解得: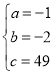 ,
,
∴y关于x的函数关系式为![]() ;
;
不选另外两个函数的理由:
∵点(0,49)不可能在反比例函数图象上,
∴y不是x的反比例函数;
∵点(-4,41),(-2,49),(2,41)不在同一直线上,
∴y不是x的一次函数;
(2)由(1)得:![]() .
.
∵![]() ,
,
∴当![]() 时,y有最大值为50,
时,y有最大值为50,
即当温度为-1℃时,这种作物每天高度增长量最大;
(3)![]()
![]() 天内要使该植物高度增长量的总和超过
天内要使该植物高度增长量的总和超过![]() ,
,
![]() 平均每天该植物高度增长量超过
平均每天该植物高度增长量超过![]() ,
,
当![]() 时,
时,![]() ,
,
整理得,![]() ,
,
解得![]() ,
,![]() ,
,
![]() 在10天内要使该植物高度增长量的总和超过
在10天内要使该植物高度增长量的总和超过![]() ,实验室的温度应保持在
,实验室的温度应保持在![]() .
.

【题目】问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?此时,显然能搭成一种等腰三角形.所以,当n=3时,m=1
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形,所以,当n=4时,m=0
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形,所以,当n=5时,m=1
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=6时,m=1
综上所述,可得表①
n | 3 | 4 | 5 | 6 |
m | 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(只需把结果填在表②中)
n | 7 | 8 | 9 | 10 |
m |
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
解决问题:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设n分别等于4k﹣1、4k、4k+1、4k+2,其中k是整数,把结果填在表 ③中)
n | 4k﹣1 | 4k | 4k+1 | 4k+2 |
m |
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)其中面积最大的等腰三角形每个腰用了 根木棒.(只填结果)