题目内容
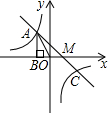 如图,已知反比例函数
如图,已知反比例函数 的图象经过第二象限内的点A(-2,m),AB⊥x轴于B,△AOB的面积为3,
的图象经过第二象限内的点A(-2,m),AB⊥x轴于B,△AOB的面积为3,
(1)求k,m的值;
(2)若直线y=ax+b经过点A,并且经过反比例函数 的图象上另一点
的图象上另一点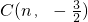 .
.
①求直线y=ax+b的解析式;
②设直线y=ax+b与x轴交于点M,求AM的长;
③根据图象写出使反比例函数 >y=ax+b的值x的取值范围.
>y=ax+b的值x的取值范围.
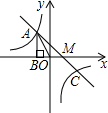 解:(1)∵点A(-2,m)在第二象限内
解:(1)∵点A(-2,m)在第二象限内∴AB=m,OB=2
∴
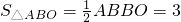
即:∴
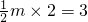 ,解得m=3
,解得m=3∴A(-2,3)
∵点A(-2,3)在反比例函数
 的图象上,
的图象上,∴
 ,解得:k=-6;
,解得:k=-6;(2)由(1)知,反比例函数为
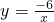 ,
,又∵反比例函数
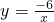 的图象经过
的图象经过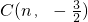
∴
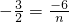 ,
,解得:n=4.
∴
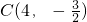
①∵直线y=ax+b过点A(-2,3)、
∴
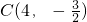
∴
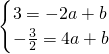
解方程组得
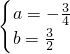 ∴直线y=ax+b的解析式为
∴直线y=ax+b的解析式为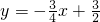 .
.②当y=0时,即
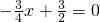 ,解得:x=2,即点M(2,0)
,解得:x=2,即点M(2,0)在Rt△ABM中,∵AB=3,BM=BO+OM=2+2=4
由勾股定理得:AM=5.
③由图象知:当-2<x<0或x>4时,
反比例函数
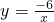 的值>
的值>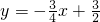 的值.
的值.分析:(1)利用△AOB的面积可求出点A的坐标,把点A的坐标代入反比例函数解析式即可求得k的值;
(2)把C坐标代入反比例函数就能求得C完整的坐标:
①把A、C代入一次函数解析式就能求得解析式;
②求出M的坐标,利用勾股定理即可求得AM长;
③应从A、C两点入手,判断出反比例函数
 的值>y=ax+b的值x的取值范围.
的值>y=ax+b的值x的取值范围.点评:过某个点,这个点的坐标应适合这个函数解析式.求一次函数的解析式需知道它上面的两个点的坐标;求自变量的取值范围应该从交点入手思考;需注意反比例函数的自变量不能取0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=