Question

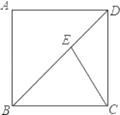
【题目】如图,在正方形ABCD中,BC=2,E是对角线BD上的一点,且BE=AB.求△EBC的面积．

Answer 1

【答案】△EBC的面积为

【解析】试题分析：作EF⊥BC于F，则∠EFB=90°，由正方形的性质得出AB=BC=2，∠DAB=∠ABC=90°，∠ABD=∠DBC=45°，得出△BEF是等腰直角三角形，因此EF=BF，由勾股定理得出EF=BF=BE=，△EBC的面积=BCEF，即可得出结果．

试题解析：作EF⊥BC于F，如图所示：

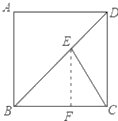
则∠EFB=90°，

∵四边形ABCD是正方形，

∴AB=BC=2，∠DAB=∠ABC=90°，

∴∠ABD=∠DBC=∠ABC=45°，

∴△BEF是等腰直角三角形，

∴EF=BF，

∵BE=AB，

∴BE=BC=2，

∴EF=BF=BE=，

∴△EBC的面积=BCEF=×2×=．