Question

【题目】如图，已知直线l：y=﹣ x+3分别与x、y轴交于点A和B．

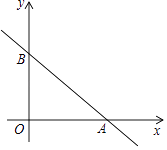
（1）求△AOB的面积；
（2）求原点O到直线l的距离．

Answer 1

【答案】
（1）解：当x=0时，y=﹣ x+3=3，

∴点B的坐标为（0，3）；

当y=﹣ x+3=0时，x=4，

∴点A的坐标为（4，0），

∴OA=4，OB=3，

∴S△AOB= OAOB= ×4×3=6

（2）解：设原点O到直线l的距离为h．

在Rt△AOB中，OA=4，OB=3，∠AOB=90°，

∴AB= =5．

由面积法可得：h= = ．

∴原点O到直线l的距离为

【解析】（1）根据直线l的解析式利用一次函数图象上点的坐标特征可求出点A、B的坐标，再利用三角形的面积公式即可求出△AOB的面积；（2）设原点O到直线l的距离为h，在Rt△AOB中，利用勾股定理即可求出AB的长度，再根据△AOB的面积利用面积法即可求出原点O到直线l的距离．

【考点精析】掌握一次函数的性质是解答本题的根本，需要知道一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小．