题目内容
【题目】如图,在△ABC中,AB=AC,,点D是边AB上一点,E为AC的中点,过点C作CF∥AB, 交DE的延长线于点F。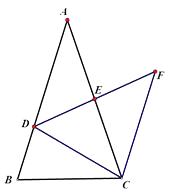
(1)求证:DE=FE;
(2)若CD=CF,∠A=40°,求∠BCD的度数。
【答案】
(1)证明:∵CF∥AB
∴∠A=∠FCE
∵E为AC的中点
∴AE=EC
∵∠AED=∠CEF
∴△AED≌△CEF
∴DF=FE
(2)∵AB=AC,∠A=40°
∴∠ACB=70°
∵CD=CF , DE=FE
∴∠DCE=∠FCE=40°
∴∠BCD=30°
【解析】(1)根据CF∥AB可得∠A=∠FCE,再由已知E为AC的中点得到AE=EC,隐含着对顶角,因此根据ASA判定△AED≌△CEF,由全等三角形的性质得证;(2)根据等腰三角形的内角的关系,利用角的和差计算即可.

练习册系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c,其自变量x与函数y的对应值如下表:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
则下列说法正确的是( )
A. 抛物线的开口向下 B. 当x>-3时,y随x的增大而增大
C. 二次函数的最小值是-2 D. 抛物线的对称轴是直线x=-![]() .
.
