题目内容
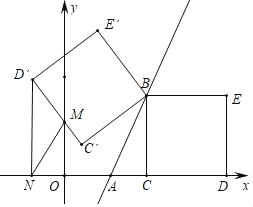
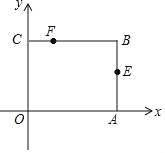
【题目】如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1,若M为x轴上的动点,N为y轴上的动点,则四边形MNFE的周长最小值是_____.
【答案】5+![]()
【解析】
作点E关于x轴的对称点E′,作点F关于y轴的对称点F′,连接E′F′,分别与x轴、y轴交于点M、N,连接FN、NM、ME,此时四边形MNFE的周长最小.根据勾股定理和轴对称性质可求解.
解:由图可得;E(3,1);F(1,2)
如图,作点E关于x轴的对称点E′,作点F关于y轴的对称点F′,连接E′F′,分别与x轴、y轴交于点M、N,连接FN、NM、ME,此时四边形MNFE的周长最小.
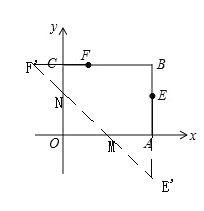
∴E′(3,﹣1),F′(﹣1,2),
设直线E′F′的解析式为y=kx+b,
有![]() 解这个方程组,
解这个方程组,
得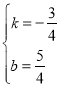
∴直线E′F′的解析式为![]() .
.
当y=0时,x=![]() ,
,
∴M点的坐标为(![]() ,0).
,0).
当x=0时,y=![]() ,
,
∴N点的坐标为(0,![]() ).
).
∵E与E′关于x轴对称,F与F′关于y轴对称,
∴NF=NF′,ME=ME′.F′B=4,E′B=3.
在Rt△BE′F′中,F′E′=![]()
∴FN+NM+ME=F′N+NM+ME′=F′E′=5.
在Rt△BEF中,EF=![]() .
.
∴FN+NM+ME+EF=5+![]() ,
,
即四边形MNFE的周长最小值是5+![]() .
.
故答案为:5+![]()

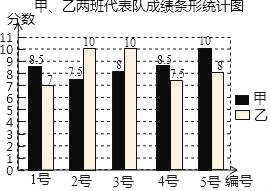
【题目】甲、乙两班分别选5名同学组成代表队参加学校组织的“国防知识”选拔赛,现根据成绩(满分10分)制作如图统计图和统计表(尚未完成)
甲、乙两班代表队成绩统计表
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | a | 0.7 |
乙班 | 8.5 | b | 10 | 1.6 |
请根据有关信息解决下列问题:
(1)填空:a= ,b= ;
(2)学校预估如果平均分能达8.5分,在参加市团体比赛中即可以获奖,现应选派 代表队参加市比赛;(填“甲”或“乙”)
(3)现将从成绩满分的3个学生中随机抽取2人参加市国防知识个人竞赛,请用树状图或列表法求出恰好抽到甲,乙班各一个学生的概率.