Question

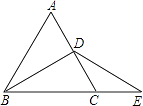
【题目】已知：如图，在ABCD中，E，F分别是边AD，BC上的点，且AE=CF，直线EF分别交BA的延长线、DC的延长线于点G，H，交BD于点O．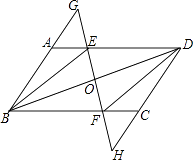
（1）求证：△ABE≌△CDF；
（2）连接DG，若DG=BG，则四边形BEDF是什么特殊四边形？请说明理由．

Answer 1

【答案】
（1）证明：∵四边形ABCD是平行四边形，

∴AB=CD，∠BAE=∠DCF，

在△ABE和△CDF中， ，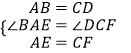

∴△ABE≌△CDF（SAS）

（2）解：四边形BEDF是菱形；理由如下：如图所示：

∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC，

∵AE=CF，

∴DE=BF，

∴四边形BEDF是平行四边形，

∴OB=OD，

∵DG=BG，

∴EF⊥BD，

∴四边形BEDF是菱形．

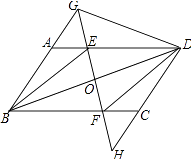
【解析】（1）由平行四边形的性质得出AB=CD，∠BAE=∠DCF，由SAS证明△ABE≌△CDF即可；（2）由平行四边形的性质得出AD∥BC，AD=BC，证出DE=BF，得出四边形BEDF是平行四边形，得出OB=OD，再由等腰三角形的三线合一性质得出EF⊥BD，即可得出四边形BEDF是菱形．