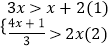题目内容
【题目】如图,已知一次函数y= ![]() x﹣3与反比例函数y=
x﹣3与反比例函数y= ![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为 , k的值为;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数y= ![]() 的图象,当y≥﹣2时,请直接写出自变量x的取值范围.
的图象,当y≥﹣2时,请直接写出自变量x的取值范围.
【答案】
(1)3;12
(2)
解:∵一次函数y= ![]() x﹣3与x轴相交于点B,
x﹣3与x轴相交于点B,
∴ ![]() x﹣3=0,
x﹣3=0,
解得x=2,
∴点B的坐标为(2,0),
如图,过点A作AE⊥x轴,垂足为E,
过点D作DF⊥x轴,垂足为F,
∵A(4,3),B(2,0),
∴OE=4,AE=3,OB=2,
∴BE=OE﹣OB=4﹣2=2,
在Rt△ABE中,
AB= ![]() =
= ![]() =
= ![]() ,
,
∵四边形ABCD是菱形,
∴AB=CD=BC= ![]() ,AB∥CD,
,AB∥CD,
∴∠ABE=∠DCF,
∵AE⊥x轴,DF⊥x轴,
∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
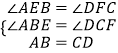 ,
,
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3,
∴OF=OB+BC+CF=2+ ![]() +2=4+
+2=4+ ![]() ,
,
∴点D的坐标为(4+ ![]() ,3)
,3)
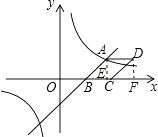
(3)
解:当y=﹣2时,﹣2= ![]() ,解得x=﹣6.
,解得x=﹣6.
故当y≥﹣2时,自变量x的取值范围是x≤﹣6或x>0.
故答案为:3,12.
【解析】解:(1)把点A(4,n)代入一次函数y= ![]() x﹣3,可得n=
x﹣3,可得n= ![]() ×4﹣3=3;
×4﹣3=3;
把点A(4,3)代入反比例函数y= ![]() ,可得3=
,可得3= ![]() ,
,
解得k=12.
【考点精析】关于本题考查的反比例函数的性质和勾股定理的概念,需要了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题: 频率分布表
分数段 | 频数 | 频率 |
50.5﹣60.5 | 16 | 0.08 |
60.5﹣70.5 | 40 | 0.2 |
70.5﹣80.5 | 50 | 0.25 |
80.5﹣90.5 | m | 0.35 |
90.5﹣100.5 | 24 | n |

(1)这次抽取了名学生的竞赛成绩进行统计,其中:m= , n=;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?