Question

如图，已知Rt△ABC中，∠C=90°．沿DE折叠，使点A与点B重合，折痕为DE．
（1）若DE=CE，求∠A的度数；
（2）若BC=6，AC=8，求CE的长．

Answer 1

分析：（1）利用翻折变换的性质得出DE垂直平分AB，进而得出∠1=∠2=∠A即可得出答案；
（2）利用勾股定理得出CE的长，即可得出CD的长．

解答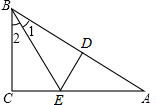：解：（1）∵折叠使点A与点B重合，折痕为DE．
∴DE垂直平分AB．
∴AE=BE，
∴∠A=∠2，
又∵DE⊥AB，∠C=90°，DE=CE，
∴∠1=∠2，
∴∠1=∠2=∠A．   
由∠A+∠1+∠2=90°，
解得：∠A=30°；

（2）设CE=x，则AE=BE=8-x． 
在Rt△BCE中，由勾股定理得：
BC²+CE ²=BE²．
即  6²+x²=（8-x）²，
解得：x=

7

4

，
即CD=

7

4

．

点评：此题主要考查了翻折变换的性质以及勾股定理，根据已知熟练应用勾股定理得出是解题关键．