题目内容
如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为D,直线AC交⊙C于点E、F,且CF=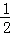 AC.
AC.
(1)求∠ACB的度数;
(2)若AC=8,求△ABF的面积.
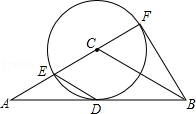
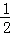 AC.
AC.(1)求∠ACB的度数;
(2)若AC=8,求△ABF的面积.

(1)∠ACB=120°.
(2)24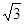
(2)24
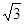
试题分析:(1)连接DC,由AB是⊙C的切线,可知CD⊥AB,根据CD=
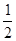 AC,得出∠A=30°,又AC=BC,从而可求得∠ACB的度数.
AC,得出∠A=30°,又AC=BC,从而可求得∠ACB的度数.(2)由(1)可得∠ACD=∠BCD=∠BCF,从而可得△ACD≌△BCF,求得∠AFB=90°,已知AC=8,根据已知求得AF=12,由于∠A=30°得出BF=
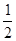 AB,由勾股定理求得BF的长,从而可求得三角形的面积.
AB,由勾股定理求得BF的长,从而可求得三角形的面积.试题解析:(1)连接CD,
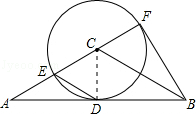
∵AB是⊙C的切线,
∴CD⊥AB,
∵CF=
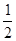 AC,CF=CE,
AC,CF=CE,∴AE=CE,
∴ED=
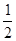 AC=EC,
AC=EC,∴ED=EC=CD,
∴∠ECD=60°,
∴∠A=30°,
∵AC=BC,
∴∠ACB=120°.
(2)∵∠A=30°,AC=BC,
∴∠ABC=30°,
∴∠BCE=60°,
在△ACD与△BCF中
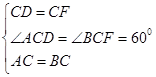
∴△ACD≌△BCF(SAS)
∴∠ADC=∠BFC,
∵CD⊥AB,
∴CF⊥BF,
∵AC=8,CF=
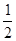 AC.
AC.∴CF=4,
∴AF=12,
∵∠AFB=90°,∠A=30°,
∴BF=
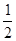 AB,
AB,设BF=x,则AB=2x,
∵AF2+BF2=AB2,
∴(2x)2﹣x2=122
解得:x=4
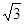
即BF=4
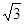
∴S△ABF=
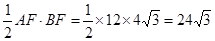

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
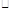 ABCD的面积之比.
ABCD的面积之比.
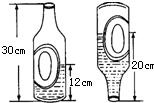
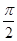
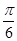
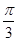
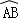 的中点,连接AC、BC,则图中阴影部分面积是( )
的中点,连接AC、BC,则图中阴影部分面积是( )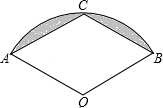
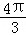 ﹣2
﹣2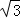 B.
B.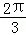 ﹣2
﹣2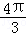 ﹣
﹣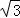 D.
D.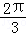 ﹣
﹣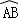 的半径OA长是6米,点C是OA的中点,点D在
的半径OA长是6米,点C是OA的中点,点D在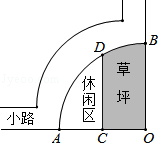
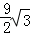 )米
)米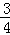 π+
π+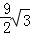 )米
)米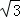 )米
)米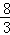 cm
cm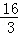 cm
cm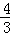 cm
cm =
=