题目内容
已知抛物线M：y=-x2+2mx+n（m，n为常数，且m＞0，n＞0）的顶点为A，与y轴交于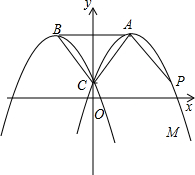
点C；抛物线N与抛物线M关于y轴对称，其顶点为B，连接AC，BC，AB．问抛物线M上是否存在点P，使得四边形ABCP为菱形？如果存在，请求出m的值；如果不存在，请说明理由．
说明：
（1）如果你反复探索，没有解决问题，请写出探索过程（要求至少写3步）；
（2）在你完成（1）之后，可以从①、②中选取一个条件，完成解答（选取①得7分；选取②得10分）．
①n=1；②n=2．
分析：可假设存在这样的P点，根据四边形ABCP是菱形，可得出AB=BC=AP，根据抛物线的对称性可得出AC=AP，因此AC=AP=PC，三角形ACP为等边三角形，可根据抛物线M的坐标求出A、C的坐标，如果连接CP，过A作x轴的垂线，垂足为D，交CP于E；那么根据C、A的坐标，即可求出CE、AE的长，然后根据∠ACE=60°，用三角函数即可得出关于m的方程，进而可求出m的值．
解答：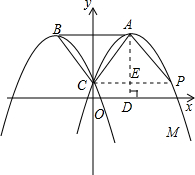
解：假设抛物线M上存在点P，使得四边形ABCP为菱形，连接CP，作AD⊥x轴于D，交CP于E，
则AD为抛物线M的对称轴，且PC=AB=BC=AP
∵由抛物线的对称性可得AC=AP，
∴AP=PC=AC．
从而△APC为等边三角形
∴∠ACE=60°
∵由抛物线M配方得，y=-x2+2mx+n=-（x-m）2+m2+n
点A、C的坐标分别为A（m，m2+n）、C（0，n），
∴AE=m2+n-n=m2，CE=m．
在Rt△ACE中，tan60°=
=
=
∴|m|=
∵m＞0
∴m=
∴抛物线M上存在点P，使得四边形ABCP为菱形，此时m=
．
解：假设抛物线M上存在点P，使得四边形ABCP为菱形，连接CP，作AD⊥x轴于D，交CP于E，则AD为抛物线M的对称轴，且PC=AB=BC=AP
∵由抛物线的对称性可得AC=AP，
∴AP=PC=AC．
从而△APC为等边三角形
∴∠ACE=60°
∵由抛物线M配方得，y=-x2+2mx+n=-（x-m）2+m2+n
点A、C的坐标分别为A（m，m2+n）、C（0，n），
∴AE=m2+n-n=m2，CE=m．
在Rt△ACE中，tan60°=
| AE |
| CE |
| m2 |
| m |
| 3 |
∴|m|=
| 3 |
∵m＞0
∴m=
| 3 |
∴抛物线M上存在点P，使得四边形ABCP为菱形，此时m=
| 3 |
点评：本题主要考查了二次函数的性质，轴对称图形以及菱形的性质等知识点．根据抛物线的对称性得出三角形ACP是等边三角形是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
正半轴交于点C．如果x1、x2是方程x2-x-6=0的两个根（x1＜x2），且△ABC的面积为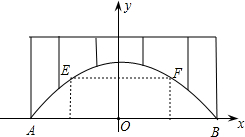
廊桥是我国古老的文化遗产．如图，是某座抛物线型的廊桥示意图，已知抛物线的函数表达式为y=-