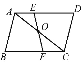
题目内容
【题目】某商场计划用![]() 元从厂家购进
元从厂家购进![]() 台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入
台新型电子产品,已知该厂家生产甲、乙、丙三种不同型号的电子产品,设甲、乙型设备应各买入![]() 台,其中每台的价格、销售获利如下表:
台,其中每台的价格、销售获利如下表:
甲型 | 乙型 | 丙型 | |
价格(元/台) |
|
|
|
销售获利(元/台) |
|
|
|
![]() 购买丙型设备 台(用含
购买丙型设备 台(用含![]() 的代数式表示) ;
的代数式表示) ;
![]() 若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了
若商场同时购进三种不同型号的电子产品(每种型号至少有一台),恰好用了![]() 元,则商场有哪几种购进方案?
元,则商场有哪几种购进方案?
![]() 在第
在第![]() 题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
题的基础上,为了使销售时获利最多,应选择哪种购进方案?此时获利为多少?
【答案】(1) ![]() ; (2) 购进方案有三种,分别为:方案一:甲型
; (2) 购进方案有三种,分别为:方案一:甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台;方案二:甲型
台;方案二:甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台;方案三:甲型
台;方案三:甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台;(3) 购进甲型
台;(3) 购进甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台,获利最多,为
台,获利最多,为![]() 元
元
【解析】
(1)用总台数减去甲、乙两型的数量及得丙的数量;
(2)根据总费用恰好是56000元可列写一个等式方程,其中包含2个未知数,仅能得出x、y之间的关系式:![]() .再利用x、y都是正数,可得y必须是5的倍数;
.再利用x、y都是正数,可得y必须是5的倍数;
(3)在(2)中得出的几种方案中,分别求解利润,得出利润最多的情况
解:![]()
![]() 由题意得,
由题意得,![]()
化简整理得:![]()
![]()
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
![]() 购进方案有三种,分别为:
购进方案有三种,分别为:
方案一:甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台;
台;
方案二:甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台;
台;
方案三:甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台.
台.
![]() 方案一:
方案一:![]() (元),故可获利
(元),故可获利![]() 元,
元,
方案二一:![]() (元),故可获利
(元),故可获利![]() 元,
元,
方案三:![]() (元),故可获利
(元),故可获利![]() 元,
元,
因为![]()
所以购进甲型![]() 台,乙型
台,乙型![]() 台,丙型
台,丙型![]() 台,获利最多,为
台,获利最多,为![]() 元.
元.

 天天练口算系列答案
天天练口算系列答案【题目】某校1200名学生参加了一场“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,整理并制作了如图所示的图表(部分未完成),请根据图表提供的信息,解答下列问题:
分数段 | 频数 | 频率 |
| 30 | 0.1 |
| 90 |
|
|
| 0.4 |
| 60 | 0.2 |
(Ⅰ)本次调查的样本容量为______;
(Ⅱ)在表中,![]() ______,
______,![]() ______;
______;
(Ⅲ)补全频数分布直方图;

(Ⅳ)如果比赛成绩80分以上(含80分)为优秀,本次竞赛中笔试成绩为优秀的大约有多少名学生?
【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术饰品 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?