ЬтФПФкШн
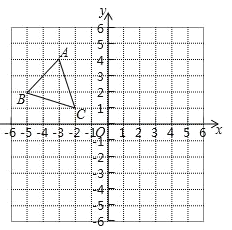
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯп![]() гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌЙ§ЕуBЕФжБЯпНЛxжсгкCЃЌЧв
гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌЙ§ЕуBЕФжБЯпНЛxжсгкCЃЌЧв![]() УцЛ§ЮЊ10.
УцЛ§ЮЊ10.
ЃЈ1ЃЉЧѓЕуCЕФзјБъМАжБЯпBCЕФНтЮіЪНЃЛ
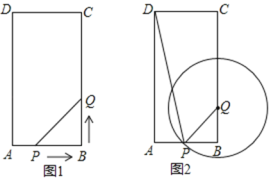
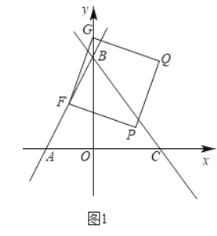
ЃЈ2ЃЉШчЭМ1ЃЌЩшЕуFЮЊЯпЖЮABжаЕуЃЌЕуGЮЊyжсЩЯвЛЖЏЕуЃЌСЌНгFGЃЌвдFGЮЊБпЯђFGгвВрзїе§ЗНаЮFGQPЃЌдкGЕуЕФдЫЖЏЙ§ГЬжаЃЌЕБЖЅЕуQТфдкжБЯпBCЩЯЪБЃЌЧѓЕуGЕФзјБъЃЛ
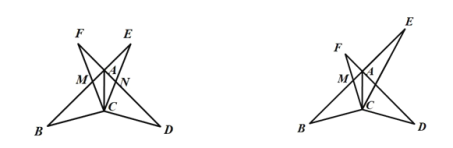
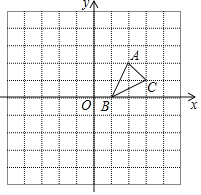
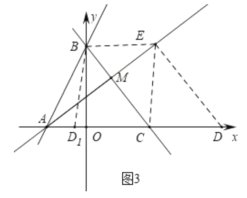
ЃЈ3ЃЉШчЭМ2ЃЌШєMЮЊЯпЖЮBCЩЯвЛЕуЃЌЧвТњзу![]() ЃЌЕуEЮЊжБЯпAMЩЯвЛЖЏЕуЃЌдкxжсЩЯЪЧЗёДцдкЕуDЃЌЪЙвдЕуDЁЂEЁЂBЁЂCЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуDЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЃЌЕуEЮЊжБЯпAMЩЯвЛЖЏЕуЃЌдкxжсЩЯЪЧЗёДцдкЕуDЃЌЪЙвдЕуDЁЂEЁЂBЁЂCЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуDЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.

ЁОД№АИЁПЃЈ1ЃЉC(3,0)ЃЛy=![]() ЃЛЃЈ2ЃЉGЕузјБъЮЊG(0,
ЃЛЃЈ2ЃЉGЕузјБъЮЊG(0,![]() ),G(0,
),G(0,![]() )ЃЛЃЈ3ЃЉDЕузјБъЮЊ(
)ЃЛЃЈ3ЃЉDЕузјБъЮЊ(![]() ,0)Лђ (
,0)Лђ (![]() ,0) Лђ(
,0) Лђ(![]() ,0)
,0)
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУШ§НЧаЮУцЛ§ЙЋЪНЧѓГіЕуCзјБъЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтЮіЪНМДПЩЃЛ
ЃЈ2ЃЉЗжСНжжЧщПіЃКЂйЕБnЃО2ЪБЃЌШчЭМ2-1жаЃЌЕуQТфдкBCЩЯЃЌЙ§GЕузїжБЯпЦНаагкxжсЃЌЙ§ЕуFЁЂQзїИУжБЯпЕФДЙЯпЃЌДЙзуЗжБ№ЮЊMЁЂNЃЌЧѓГіQ(n-2ЃЌn-1).ЂкЕБnЃМ2ЪБЃЌШчЭМ2-2ЃЌЭЌРэПЩЕУQ(2-nЃЌn+1)ЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтМДПЩЃЛ
ЃЈ3ЃЉРћгУШ§НЧаЮУцЛ§ЙЋЪНЧѓГіMзјБъЃЌДгЖјЧѓГіжБЯпAMЕФНтЮіЪНЃЌзїBEЁЮOCНЛAMгкEЃЌЕБCD=BEЪБПЩЕУЫФБпаЮBCDEЃЌЫФБпаЮBECD1ЪЧЦНааЫФБпаЮЃЌШЛКѓНјвЛВНЕУГіИїЕузјБъ.
ЃЈ1ЃЉЁпжБЯпy=2x+4гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌ
ЁрA(-2,0)ЃЌB(0,4)ЃЌ
ЁрOA=2ЃЌOB=4ЃЌ
ЁпSЁїABC=![]() ACOB=10ЃЌ
ACOB=10ЃЌ
ЁрAC=5ЃЌ
ЁрOC=3ЃЌ
ЁрC(3,0)ЃЌ
ЩшжБЯпBCНтЮіЪНЮЊy=kx+bЃЌ
дђЃК3k+b=0ЃЌb=4ЃЌ
Ёрk=![]() ЃЌ
ЃЌ
ЁржБЯпBCНтЮіЪНЮЊy=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпFA=FBЃЌA(-2,0)ЃЌB(0,4)ЃЌ
ЁрF(-1,2)ЃЌЩшG(0,n)ЃЌ
ЕБnЃО2ЪБЃЌШчЭМ2-1ЫљЪОЃЌЕуQТфдкBCЩЯЪБЃЌЙ§GзїжБЯпЦНаагкxжсЃЌЙ§ЕуFЁЂQзїИУжБЯпЕФДЙЯпЃЌДЙзуЗжБ№ЮЊMЁЂNЃЌ
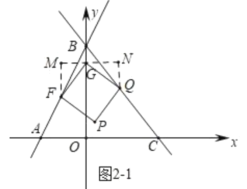
ЁпЫФБпаЮFGQPЪЧе§ЗНаЮЃЌ
ЁрЁїFMGЁеЁїGNQЃЌ
ЁрMG=NQ=1ЃЌFM=GN=n-2ЃЌ
ЁрQ(n-2ЃЌn-1)ЃЌ
ЁпQЕудкжБЯпy=![]() ЩЯЃЌ
ЩЯЃЌ
Ёрn-1=![]() ЃЌ
ЃЌ
Ёрn=![]() ЃЌ
ЃЌ
ЁрG(0,![]() ),
),
ЕБnЃМ2ЪБЃЌШчЭМ2-2ЃЌЭЌРэПЩЕУЃКQ(2-nЃЌn+1)ЃЌ

ЁпQЕудкжБЯпy=![]() ЩЯЃЌ
ЩЯЃЌ
Ёрn+1=![]() ЃЌ
ЃЌ
Ёрn=![]() ЃЌ
ЃЌ
ЁрG(0,![]() ),
),
злЩЯЫљЪіЃЌGЕузјБъЮЊG(0,![]() ),G(0,
),G(0,![]() )ЃЛ
)ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЩшM(m,![]() )ЃЌ
)ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁрM(![]() ,
,![]() )ЃЌ
)ЃЌ
ЁржБЯпAMЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
зїBEЁЮOCНЛжБЯпAMгыEЃЌДЫЪБE(![]() ,4)ЃЌ
,4)ЃЌ
ЕБCD=BEЪБЃЌЫФБпаЮBCDEЃЌЫФБпаЮBECD1ЪЧЦНааЫФБпаЮЃЌ
ПЩЕУЃКD(![]() ,0)ЃЌD1(
,0)ЃЌD1(![]() ,0)ЃЌ
,0)ЃЌ
ИљОнЖдГЦадПЩЕУDЙигкAЕФЖдГЦЕуD2(![]() ,0)вВЗћКЯЬѕМўЃЌ
,0)вВЗћКЯЬѕМўЃЌ
злЩЯЫљЪіЃЌDЕузјБъЮЊЃК(![]() ,0)Лђ (
,0)Лђ (![]() ,0) Лђ(
,0) Лђ(![]() ,0)
,0)

 ПкЫугыгІгУЬтПЈЯЕСаД№АИ
ПкЫугыгІгУЬтПЈЯЕСаД№АИ УћЪІЕуОІзжДЪОфЖЮЦЊЯЕСаД№АИ
УћЪІЕуОІзжДЪОфЖЮЦЊЯЕСаД№АИ