题目内容
如图,已知点A,B,C,D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周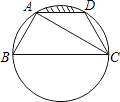 长为10cm.
长为10cm.(1)求此圆的半径;
(2)求图中阴影部分的面积(其中л≈3,
| 3 |
分析:(1)根据平行线的性质以及角平分线的定义,得∠CAD=∠ACD=∠ACB=30°.再根据圆周角定理的推论得到弧AB=弧AD=弧CD,则AB=AD=CD,同时根据角的度数可以求得∠BAC=90°,根据直角三角形30度所对的直角边是斜边的一半,求得BC=2AD,再根据四边形的周长列方程计算;
(2)由(1)可以发现BC是直径,设其圆心是O,连接OA,OD,根据两条平行线间的距离处处相等,得到三角形AOD的面积等于三角形ACD的面积,则阴影部分的面积等于扇形OAD的面积减去三角形AOD的面积.
(2)由(1)可以发现BC是直径,设其圆心是O,连接OA,OD,根据两条平行线间的距离处处相等,得到三角形AOD的面积等于三角形ACD的面积,则阴影部分的面积等于扇形OAD的面积减去三角形AOD的面积.
解答:解:(1)∵AD∥BC,∠ADC=120°,
∴∠BCD=60°(2分)
又∵AC平分∠BCD,
∴∠DAC=∠ACB=∠DCA=30度.(4分)
∴
=
,∠B=60度.
∴∠BAC=90°,(6分)
∴BC是圆的直径,BC=2AB.(7分)
∵四边形ABCD的周长为10cm,
∴AB=AD=DC=2cm,BC=4cm.
∴此圆的半径为2cm.(8分)
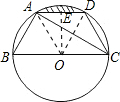
(2)设BC的中点为O,由(1)可知O即为圆心.
连接OA,OD,过O作OE⊥AD于E.(9分)
在Rt△AOE中,∠AOE=30°,
∴OE=OA•cos30°=
cm.
∴S△AOD=
×2×
=
(cm2).(10分)
∴S阴影=S扇形AOD-S△OAD=
-
=
-
≈0.3(cm2).(12分)
∴∠BCD=60°(2分)
又∵AC平分∠BCD,
∴∠DAC=∠ACB=∠DCA=30度.(4分)
∴
 |
| AB= |
 |
| AD |
 |
| CD |
∴∠BAC=90°,(6分)
∴BC是圆的直径,BC=2AB.(7分)
∵四边形ABCD的周长为10cm,
∴AB=AD=DC=2cm,BC=4cm.
∴此圆的半径为2cm.(8分)

(2)设BC的中点为O,由(1)可知O即为圆心.
连接OA,OD,过O作OE⊥AD于E.(9分)
在Rt△AOE中,∠AOE=30°,
∴OE=OA•cos30°=
| 3 |
∴S△AOD=
| 1 |
| 2 |
| 3 |
| 3 |
∴S阴影=S扇形AOD-S△OAD=
| 60×π×22 |
| 360 |
| 3 |
| 2π |
| 3 |
| 3 |
点评:此题中要通过计算角的度数,发现直角三角形和等腰三角形.根据直角三角形的性质和等腰三角形的性质进行计算.尤其是在第二问中,能够把不规则图形的面积转化为构造图形的面积.

练习册系列答案
相关题目
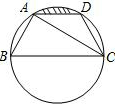 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
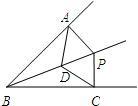 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )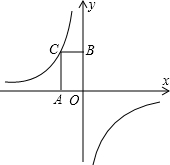 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=-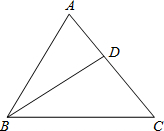 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=