题目内容
【题目】如图,平行四边形ABCD中,已知AB=6,BC=9, ![]() .对角线AC、BD交于点O.动点P在边AB上,⊙P经过点B,交线段PA于点E.设BP= x.
.对角线AC、BD交于点O.动点P在边AB上,⊙P经过点B,交线段PA于点E.设BP= x.
(1)求AC的长;
(2)设⊙O的半径为y,当⊙P与⊙O外切时,求y关于x的函数解析式,并写出定义域;
(3)如果AC是⊙O的直径,⊙O经过点E,求⊙O与⊙P的圆心距OP的长.


【答案】(1)9;(2)![]() ,定义域:0<x≤3;(3)
,定义域:0<x≤3;(3)![]() 或
或![]()
【解析】试题分析:(1)作AH⊥BC于H,根据已知条件和锐角三角函数的定义即可求得BH=2,根据勾股定理求得AH的长,在分局勾股定理求得AC的长即可;(2) 作OI⊥AB于I,联结PO,可得AO=4.5,Rt△AIO中,求得AI=1.5,IO= 3![]() ,即可得PI=
,即可得PI=![]() -x,在Rt△PIO中,根据勾股定理求得
-x,在Rt△PIO中,根据勾股定理求得![]() ,又因⊙P与⊙O外切,可得
,又因⊙P与⊙O外切,可得![]() ,所以
,所以![]() -x,因为动点P在边AB上,⊙P经过点B,交线段PA于点E,即可得定义域为0<x≤3;(3)分①当E与点A不重合时和②当E与点A重合时两种情况求AP的长即可.
-x,因为动点P在边AB上,⊙P经过点B,交线段PA于点E,即可得定义域为0<x≤3;(3)分①当E与点A不重合时和②当E与点A重合时两种情况求AP的长即可.
试题解析:
(1)作AH⊥BC于H,且![]() ,AB=6,
,AB=6,
那么![]()
BC=9,HC=9-2=7,![]() ,
,![]() ﹒
﹒
(2)作OI⊥AB于I,联结PO,AC=BC=9,AO=4.5,
∴∠OAB=∠ABC,
∴Rt△AIO中,![]() ,
,
∴AI=1.5,IO= ![]() ,
,
∴PI=AB-BP-AI=6-x-1.5= ![]() ,
,
∴Rt△PIO中,![]() ,
,
∵⊙P与⊙O外切,∴![]() ,
,
∴![]() =
= ![]() ,
,
∵动点P在边AB上,⊙P经过点B,交线段PA于点E.∴定义域:0<x≤3;
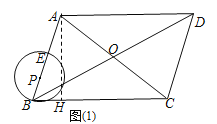
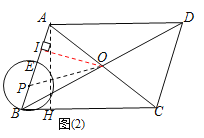
(3)由题意得:∵点E在线段AP上,⊙O经过点E,∴⊙O与⊙P相交
∵AO是⊙O半径,且AO>OI,∴交点E存在两种不同的位置,OE=OA= ![]()
①当E与点A不重合时,AE是⊙O的弦,OI是弦心距.∵AI=1.5,AE=3,∴点E是AB中点,![]() ,
,![]() ,
,![]() ,IO=
,IO= ![]()
![]() ,
,
②当E与点A重合时,点P是AB中点,点O是AC中点,![]() ,
,
∴![]() 或
或![]() .
.








