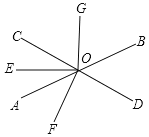
��Ŀ����
����Ŀ��һ����������������ԭ��������������ϵ�һ��һ��������������һ�����������������ľ�������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��1�����![]() ������������ô��
������������ô��![]() �������ľ�����______��
�������ľ�����______��
��2����![]() �����������λ������Ӧ����������______��
�����������λ������Ӧ����������______��
��3����![]() ������������λ����ԭ���______�ࣻ
������������λ����ԭ���______�ࣻ
��4��������ڳ����㣬���������һ��������![]() �������������ڶ���������
�������������ڶ���������![]() �������������Դ����ƣ����
�������������Դ����ƣ����![]() ������������ô��
������������ô��![]() �μ���______��
���______��
�ڻ���������������������λ����ԭ���ͬ�ࣿ
���𰸡���1��n����2��-3����3���ң���4����![]() ���ڲ��ᣬ������
���ڲ��ᣬ������
��������
��1����������ɵõ�n�������ľ���Ϊn����2��������ʽ-1+2-3+4-5= -3�ɵã���3��������ʽ-1+2-3+4-5+��+100= 50�ɵã���4���ٸ����桢ż���ı�ʾ�����ɵã�����ʽ���㣬���ݼ����������ж�.
�⣺��1���ߵ�һ�����������Ĵ������ľ���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��
���n�������ľ���Ϊ![]() ��
��
��2����������ã�![]() ��
��
���![]() �����������λ������Ӧ����������-3��
�����������λ������Ӧ����������-3��
��3����������ã�![]() ��
��
���![]() ������������λ����ԭ����Ҳࣻ
������������λ����ԭ����Ҳࣻ
��4���ٸ�������ɵã���n��nΪ��������Ϊ����ʱ����ԭ����࣬��Ϊn���෴��-n����n��nΪ��������Ϊż��ʱ����ԭ���Ҳ࣬��Ϊn��
�൱![]() ������������
������������![]() ���
���![]() .
.
�ڲ���
��ͣ�![]()
��![]() Ϊ����ʱ��ԭʽ
Ϊ����ʱ��ԭʽ![]()
��![]() Ϊż��ʱ��ԭʽ
Ϊż��ʱ��ԭʽ![]()
�ɴ˿�֪��������������ÿ����һ���������͵ķ��Ŷ���ı䣬�ʲ�����������������������λ����ԭ���ͬ��.

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д�����Ŀ����ٵ��ˣ�����ӭ���ֻ��г�������������ij�̳����ۼס�������Ʒ�Ƶ������ֻ����������ֻ��Ľ��ۺ��ۼ����±���ʾ��
�� | �� | |
���ۣ�Ԫ/���� | 4000 | 2500 |
�ۼۣ�Ԫ/���� | 4300 | 3000 |
���̳��ƻ�Ͷ��15.5��Ԫ�ʽ�ȫ�����ڹ��������ֻ����ɲ�������ȫ�����ۺ�ɻ�ë������2��Ԫ����ë����=���ۼ۩����ۣ�����������
��1�����̳�Ҫ�뾡���ܶ�Ĺ��������ֻ���Ӧ�ð��������Ľ��������������������ֻ���
��2��ͨ���г����У����̳������ڼ����ֻ��������ķ����ϣ����ټ����ֻ��Ĺ������������������ֻ��Ĺ�����������֪�����ֻ����ӵ������Ǽ����ֻ����ٵ�������2�����������ڹ����������ֻ������ʽ���16��Ԫ�����̳�����������ʹȫ�����ۺ��õ�ë�������������ë����