题目内容
【题目】如图，抛物线y=ax2+bx+1经过点（2，6），且与直线y=
x+1相交于A，B两点，点A在y轴上，过点B作BC⊥x轴，垂足为点C（4，0）．
（1）求抛物线的解析式；
（2）若P是直线AB上方该抛物线上的一个动点，过点P作PD⊥x轴于点D，交AB于点E，求线段PE的最大值；
（3）在（2）的条件，设PC与AB相交于点Q，当线段PC与BE相互平分时，请求出点Q的坐标．
【答案】（1）y=-x2+
x+1；（2）4；（3）（
，
），（
，
）．
【解析】
试题分析：（1）根据题意得出B点坐标，再利用待定系数法求出抛物线解析式；
（2）首先表示出P，E点坐标，再利用PE=PD-ED，结合二次函数最值求法进而求出PE的最大值；
（3）根据题意可得：PE=BC，则-x2+4x=3，进而求出Q点的横坐标，再利用直线上点的坐标性质得出答案．
试题解析：（1）∵BC⊥x轴，垂足为点C（4，0），且点B在直线y=
x+1上，
∴点B的坐标为：（4，3），
∵抛物线y=ax2+bx+1经过点（2，6）和点B（4，3），
∴
，
解得：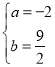
，
故抛物线的解析式为：y=-x2+x+1；
（2）如图所示：设动点P的坐标为；（x，-x2+x+1），
则点E的坐标为：（x， x+1），
∵PD⊥x轴于点D，且点P在x轴上，
∴PE=PD-ED=（-x2+x+1）-（x+1）
=-x2+4x
=-（x-2）2+4，
则当x=2时，PE的最大值为：4；
（3）∵PC与BE互相平分，
∴PE=BC，
∴-x2+4x=3，即x2-4x+3=0，
解得：x1=1，x2=3，
∵点Q分别时PC，BE的中点，且点Q在直线y=x+1，
∴①当x=1时，点Q的横坐标为：，
∴点Q的坐标为：（，），
②当x=3时，点Q的横坐标为：，
∴点Q的坐标为：（，），
综上所述，点Q的坐标为：（，），（，）．
