��Ŀ����
����Ŀ���ı���ABCD �У�AB=3��BC=4��E��F �ǶԽ��� AC�ϵ��������㣬�ֱ�� A��C ͬʱ������ ������У��ٶȾ�Ϊ 1cm/s���˶�ʱ��Ϊ t �룬������һ�����㵽����ֹͣ�˶���
��1���� G��H �ֱ��� AB��DC �е㣬��֤���ı��� EGFH ʼ����ƽ���ı��Σ�
��2���ڣ�1�������£��� t Ϊ��ֵʱ���ı��� EGFH Ϊ���Σ�
��3���� G��H �ֱ������� A��B��C��C��D��A �ϵĶ��㣬�� E��F ��ͬ���ٶ�ͬʱ�������� t Ϊ��ֵʱ���ı��� EGFH Ϊ���Σ�

���𰸡���1��֤����������
��2���� t Ϊ0.5s��4.5sʱ���ı��� EGFH Ϊ���Σ�
��3��tΪ![]() sʱ���ı���EGFHΪ����.
sʱ���ı���EGFHΪ����.
�������������������1���ɾ��ε����ʵó�AB=CD��AB��CD��AD��BC����B=90�㣬�ɹ��ɶ������AC=5����SAS֤����AFG�ա�CEH���ó�GF=HE��ͬ���ó�GE=HF�����ɵó����ۣ�
��2����֤���ı���BCHG��ƽ���ı��Σ��ó�GH=BC=4�����Խ���EF=GH=4ʱ��ƽ���ı���EGFH�Ǿ��Σ��������������AE=CF=t���ó�EF=5-2t=4���ⷽ�̼��ɣ���AE=CF=t���ó�EF=5-2��5-t��=4���ⷽ�̼��ɣ�
��3������AG��CH�������ε����ʵó�GH��EF��OG=OH��OE=OF���ó�OA=OC��AG=AH��֤���ı���AGCH�����Σ��ó�AG=CG����AG=CG=x����BG=4-x���ɹ��ɶ����ó����̣��ⷽ�����BG���ó�AB+BG=![]() �����ɵó�t��ֵ��
�����ɵó�t��ֵ��
�����������1�����ı���ABCD�Ǿ��Σ�
��AB=CD��AB��CD��AD��BC����B=90����
��AC=![]() =5����GAF=��HCE��
=5����GAF=��HCE��
��G��H�ֱ���AB��DC�е㣬
��AG=BG��CH=DH��
��AG=CH��
��AE=CF��
����AFG����CEH��
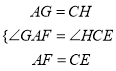
���AFG�ա�CEH��SAS����
��GF=HE��
ͬ����GE=HF��
���ı���EGFH��ƽ���ı��Σ�
��2���ɣ�1���ã�BG=CH��BG��CH��
���ı���BCHG��ƽ���ı��Σ�
��GH=BC=4����EF=GH=4ʱ��ƽ���ı���EGFH�Ǿ��Σ������������
��AE=CF=t��EF=5��2t=4����ã�t=0.5��
��AE=CF=t��EF=5��2��5��t��=4����ã�t=4.5��
������������tΪ0.5s��4.5sʱ���ı���EGFHΪ���Σ�
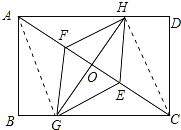
��3������AG��CH����ͼ��ʾ��
���ı���EGFHΪ���Σ�
��GH��EF��OG=OH��OE=OF��
��OA=OC��AG=AH��
���ı���AGCH�����Σ�
��AG=CG��
��AG=CG=x����BG=4��x���ɹ��ɶ����ã�AB2+BG2=AG2����32+��4��x��2=x2��
��ã�x=![]() ��
��
��BG=4��![]() =
=![]() ��
��
��AB+BG=3+![]() =
=![]() ��
��
��tΪ![]() sʱ���ı���EGFHΪ���Σ�
sʱ���ı���EGFHΪ���Σ�

 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д� Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�