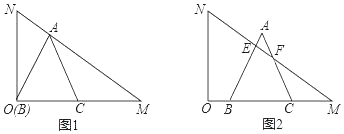Question

【题目】（1）问题发现：如图1，在等边△ABC中，点D为BC边上一动点，DE∥AB交AC于点E，将AD绕点D顺时针旋转60°得到DF，连接CF．则AE与FC的数量关系是　 　；∠ACF的度数为　 　．

（2）拓展探究：如图2，在Rt△ABC中，∠ABC＝90°，∠ACB＝60°，点D为BC边上一动点，DE∥AB交AC于点E，当∠ADF＝∠ACF＝90°时，求的值．

（3）解决问题：如图3，在△ABC中，BC：AB＝m，点D为BC的延长线上一点过点D作DE∥AB交AC的延长线于点E，直接写出当∠ADF＝∠ACF＝∠ABC时，的值．

Answer 1

【答案】（1）AE＝CF，60°；（2）；（3）.

【解析】

（1）由题意可证△DEC是等边三角形，∠AED=120°，可得DE=DC，由旋转性质可得∠ADF=60°=∠EDC，AD=DF，由“SAS”可证△ADE≌△FDC，可得AE=CF，∠AED=∠DCF=120°，可得∠ACF=60°；

（2）通过证明△DAE∽△DFC，可得，通过证明△EDC∽△ABC，可得，即可求的值；

（3）通过证明△DAE∽△DFC，可得，通过证明△EDC∽△ABC，可得，即可求的值；

（1）∵DE∥AB

∴∠ABC＝∠EDC＝60°，∠BAC＝∠DEC＝60°

∴△DEC是等边三角形，∠AED＝120°

∴DE＝DC，

∵将AD绕点D顺时针旋转60°得到DF，

∴∠ADF＝60°＝∠EDC，AD＝DF

∴∠ADE＝∠FDC，且CD＝DE，AD＝DF

∴△ADE≌△FDC（SAS）

∴AE＝CF，∠AED＝∠DCF＝120°

∴∠ACF＝60°，

故答案为：AE＝CF，60°

（2）∵∠ABC＝90°，∠ACB＝60°，

∴∠BAC＝30°

∴tan∠BAC＝

∵DE∥AB

∴∠EDC＝∠ABC＝90°

∵∠ADF＝90°，

∴∠ADE＝∠FDC

∵∠ACF＝90°，∠AED＝∠EDC+∠ACB，∠FCD＝∠ACF+∠ACB

∴∠AED＝∠FCD，且∠ADE＝∠FDC

∴△DAE∽△DFC

∴

∵DE∥AB

∴△EDC∽△ABC

∴

∴

（3）∵AB∥DE

∴∠ABC＝∠BDE＝∠ADF，∠BAC＝∠E

∴∠BDE+∠ADB＝∠ADF+∠ADB

∴∠ADE＝∠CDF，

∵∠ACD＝∠ABC+∠BAC＝∠ACF+∠DCF，且∠ACF＝∠ABC

∴∠BAC＝∠DCF＝∠E，且∠ADE＝∠CDF

∴△ADE∽△FDC

∴

∵AB∥DE

∴△ABC∽△EDC

∴，且BC：AB＝m，

∴