题目内容

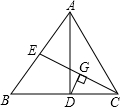
如图所示，已知在△ABC中，∠C=90°，AD=AC，DE⊥AB交BC于点E，若∠B=28°，则∠AEC=（　　）
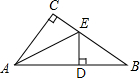
A．28°B．59°C．60°D．62°

∵在△ABC中，∠C=90°，
AD=AC，DE⊥AB交BC于点E，
∴△CAE≌△DAE，∴∠CAE=∠DAE=
1
2
∠CAB，
∵∠B+∠CAB=90°，∠B=28°，
∴∠CAB=90°-28°=62°，
∵∠AEC=90°-
1
2
∠CAB=90°-31°=59°．
故选B．
练习册系列答案
相关题目
在△ABC中，∠A：∠B：∠C=1：2：3，CD⊥AB于D，AB=a，则DB等于（　　）
A．
a
4
B．
a
3
C．
a
2
D．
3a
4
在△ABC中，下面有五个论断：
①AD是高；②CE是中线；③DC=BE；④DG⊥CE于G；⑤G是EC中点．
请你用四个作为条件，余下作为结论编一道数学问题，并写出解答过程．
如图，∠A=∠D=90°，再添加一个条件______，即可使Rt△ABC≌Rt△DCB，理由是______．
直角三角形的周长为2+
6
，斜边上的中线长为1，则该三角形的面积等于（　　）
A．1B．
1
2
C．
1
4
D．
3
4
如图，AC、BD是长方形ABCD的对角线，过点D作DE∥AC交BC的延长线于E，则图中与△ABC全等的三角形共有（　　）
A．1个B．2个C．3个D．4个
已知：在△ABC中，∠ABC=90°，点E在直线AB上，ED与直线AC垂直，垂足为D，且点M为EC中点，连接BM，DM．

（1）如图1，若点E在线段AB上，探究线段BM与DM及∠BMD与∠BCD所满足的数量关系，并直接写出你得到的结论；
（2）如图2，若点E在BA延长线上，你在（1）中得到的结论是否发生变化？写出你的猜想并加以证明；
（3）若点E在AB延长线上，请你根据条件画出相应的图形，并直接写出线段BM与DM及∠BMD与∠BCD所满足的数量关系．
如图，方格图案中的正方形顶点叫做格点，图1中以格点为顶点的等腰直角三角形有4个，图2中以格点为顶点的等腰直角三角形有10个，图3中以格点为顶点的等腰直角三角形的个数为（　　）
A．16个B．20个C．24个D．28个
如图，在格点中找到一点C，使得△ABC是等腰三角形，且AB为其中的一条腰，这样的格点共有几个？（　　）
A．2个B．3个C．4个D．5个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网