题目内容
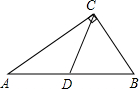
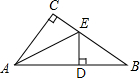
在△ABC中,∠A:∠B:∠C=1:2:3,CD⊥AB于D,AB=a,则DB等于( )
A.
| B.
| C.
| D.
|
根据题意,设∠A、∠B、∠C为k、2k、3k,
则k+2k+3k=180°,
解得k=30°,2k=60°,3k=90°,
∵AB=a,∴BC=
AB=
,
∵CD⊥AB,
∴∠BCD=∠A=30°,
∴DB=
BC=
×
=
.
故选A.
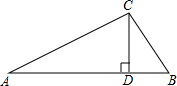
则k+2k+3k=180°,
解得k=30°,2k=60°,3k=90°,
∵AB=a,∴BC=
| 1 |
| 2 |
| a |
| 2 |
∵CD⊥AB,
∴∠BCD=∠A=30°,
∴DB=
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| a |
| 4 |
故选A.


练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目