题目内容
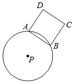
【题目】如图,圆P的半径为10,A、B是圆上任意两点,且AB=12,以AB为边作正方ABCD(点D、P在直线AB的两侧),若AB边绕点P旋转一周,则CD边扫过的面积为( ).
A.0B.36πC.![]() D.6π
D.6π
【答案】B
【解析】
连接PA、PD,过点P作PE垂直AB于点E,延长PE交CD于点F,根据垂径定理可得出AE=BE=![]() AB,利用勾股定理即可求出PE的长度,再根据平行线的性质结合正方形的性质即可得出EF=BC=AB,DF=AE,根据圆环的面积公式即可得出结论.
AB,利用勾股定理即可求出PE的长度,再根据平行线的性质结合正方形的性质即可得出EF=BC=AB,DF=AE,根据圆环的面积公式即可得出结论.
连接PA、PD,过点P作PE垂直AB于点E,延长PE交CD于点F,如图所示.
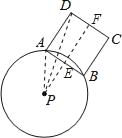
∵AB是⊙P上一弦,且PE⊥AB,
∴AE=BE=![]() AB=6,
AB=6,
∵四边形ABCD是正方形,
∴∠DAE=∠ADF=∠DFE=90°,
∴四边形AEFD是矩形,
∴DF=AE=6,
∵若AB边绕点P旋转一周,则CD边扫过的图形为以PF为内圆半径、以PD为外圆半径的圆环.
∴S=πPD2﹣πPF2=π(PD2﹣PF2)=πDF2=36π,
故选:B.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目