题目内容
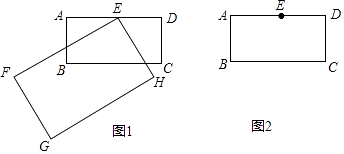
【题目】如图,点E为正方形ABCD中AD边上的一个动点,AB=16,以BE为边画正方形BEFG,边EF与边CD交于点H.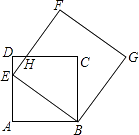
(1)当E为边AD的中点时,求DH的长;
(2)当tan∠ABE= ![]() 时,连接CF,求CF的长;
时,连接CF,求CF的长;
(3)连接CE,求△CEF面积的最小值.
【答案】
(1)
解:∵四边形ABCD和四边形BGFE是正方形,
∴∠D=∠A=∠BEF=90°,
∴∠AEB+∠DEH=∠DEH+∠DHE=90°,
∴∠AEB=∠DHE,
∴△EDH∽△BAE,
∴ ![]() ,
,
∵E为边AD的中点,
∴DE=AE=8,
∴ ![]() ,
,
∴DH=4;
(2)
解:过F作FG⊥DC于点G,FM⊥AD,交AD的延长线于M,连接CF,
∵tan∠ABE= ![]() ,AB=16,
,AB=16,
∴AE=12,
∴DE=4,
∵∠MEF+∠AEB=∠AEB+∠ABE=90°,
∴∠MEF=∠ABE,
∴tan∠MEF= ![]() ,
,
∴ME=16,FM=12,
∴DM=12,
∴DM=MF,
∴四边形DGFM是正方形,
∴FG=12,HG=9,
∴CG=4,
∴FC= ![]() =4
=4 ![]()

(3)
解:∵S△CEF=S△CHF+S△CHE= ![]() CHEM,
CHEM,
∵△EMF≌△BAE,
∴EM=AB=16,
∴S△CEF=8CH,
∵△EDH∽△BAE,
∴ ![]() ,
,
设AE为x,则DH= ![]() (﹣x2+16x)=﹣
(﹣x2+16x)=﹣ ![]() (x﹣8)2+4≤4,
(x﹣8)2+4≤4,
∴DH≤4,
∴CH≥12,CH最小值是12,
∴△CEF面积的最小值是96
【解析】(1)根据正方形的性质得到∠D=∠A=∠BEF=90°,根据余角的性质得到∠AEB=∠DHE,根据相似三角形的想知道的 ![]() ,代入数据即可得到结论;(2)过F作FG⊥DC于点G,FM⊥AD,交AD的延长线于M,连接CF,根据已知条件得到AE=12,求得DE=4,根据余角的性质得到∠MEF=∠ABE,等量代换得到tan∠MEF=
,代入数据即可得到结论;(2)过F作FG⊥DC于点G,FM⊥AD,交AD的延长线于M,连接CF,根据已知条件得到AE=12,求得DE=4,根据余角的性质得到∠MEF=∠ABE,等量代换得到tan∠MEF= ![]() 求得ME=16,FM=12,根据勾股定理即可得到结论;(3)由于S△CEF=S△CHF+S△CHE=
求得ME=16,FM=12,根据勾股定理即可得到结论;(3)由于S△CEF=S△CHF+S△CHE= ![]() CHEM,根据全等三角形的性质得到EM=AB=16,求得S△CEF=8CH,根据相似三角形的性质得到
CHEM,根据全等三角形的性质得到EM=AB=16,求得S△CEF=8CH,根据相似三角形的性质得到 ![]() ,设AE为x,于是得到DH=
,设AE为x,于是得到DH= ![]() (﹣x2+16x)=﹣
(﹣x2+16x)=﹣ ![]() (x﹣8)2+4≤4,即可得到结论.
(x﹣8)2+4≤4,即可得到结论.
【考点精析】本题主要考查了正方形的性质和相似三角形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;对应角相等,对应边成比例的两个三角形叫做相似三角形才能正确解答此题.