题目内容
【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F. 
(1)若⊙O的半径为8,求CD的长;
(2)证明:PE=PF;
(3)若PF=13,sinA= ![]() ,求EF的长.
,求EF的长.
【答案】
(1)解:连接OD,
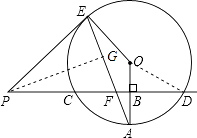
∵直线PD垂直平分⊙O的半径OA于点B,⊙O的半径为8,
∴OB= ![]() OA=4,BC=BD=
OA=4,BC=BD= ![]() CD,
CD,
∴在Rt△OBD中,BD= ![]() =4
=4 ![]() ,
,
∴CD=2BD=8 ![]()
(2)解:∵PE是⊙O的切线,
∴∠PEO=90°,
∴∠PEF=90°﹣∠AEO,∠PFE=∠AFB=90°﹣∠A,
∵OE=OA,
∴∠A=∠AEO,
∴∠PEF=∠PFE,
∴PE=PF
(3)解:过点P作PG⊥EF于点G,
∴∠PGF=∠ABF=90°,
∵∠PFG=∠AFB,
∴∠FPG=∠A,
∴FG=PFsinA=13× ![]() =5,
=5,
∵PE=PF,
∴EF=2FG=10
【解析】(1)首先连接OD,由直线PD垂直平分⊙O的半径OA于点B,⊙O的半径为8,可求得OB的长,又由勾股定理,可求得BD的长,然后由垂径定理,求得CD的长;(2)由PE是⊙O的切线,易证得∠PEF=90°﹣∠AEO,∠PFE=∠AFB=90°﹣∠A,继而可证得∠PEF=∠PFE,根据等角对等边的性质,可得PE=PF;(3)首先过点P作PG⊥EF于点G,易得∠FPG=∠A,即可得FG=PFsinA=13× ![]() =5,又由等腰三角形的性质,求得答案.
=5,又由等腰三角形的性质,求得答案.
【考点精析】关于本题考查的线段垂直平分线的性质和勾股定理的概念,需要了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案【题目】雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康,太原市会持续出现雾霾天气吗?在2016年2月周末休息期间,某校九年级1班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计图表,观察并回答下列问题:
类别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 城中村燃煤问题 | 15% |
D | 其他(绿化不足等) | n |
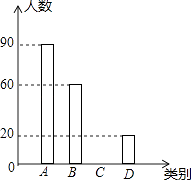
(1)请你求出本次被调查市民的人数及m,n的值,并补全条形统计图;
(2)若太原市有300万人口,请你估计持有A,B两类看法的市民共有多少人?
(3)学校要求小颖同学在A,B,C,D这四个雾霾天气的主要成因中,随机抽取两项作为课题研究的项目进行考察分析,请用画树状图或列表的方法,求出小颖同学刚好抽到B(汽车尾气排放),C(城中村燃煤问题)的概率.(用A,B,C,D表示各项目)