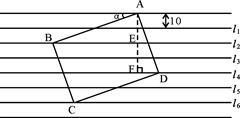
题目内容
如图:把一张给定大小的矩形卡片ABCD放在宽度为10mm的横格纸中,恰好四个顶点都在横格线上,已知α=25°,求长方形卡片的周长。(精确到1mm,参考数据: sin25°≈0,cos25°≈0.9,tan25°≈0.5).

解:作AF⊥l4,交l2于E,交l4于F
则△ABE和△AFD均为直角三角形
在Rt△ABE中,∠ABE=∠α=25°
sin∠ABE=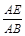 ∴AB=
∴AB=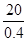 =50
=50
∵∠FAD=90°-∠BAE,∠α=90°-∠BAE
∴∠FAD=∠α=25°
在Rt△AFD中,cos∠FAD=
AD=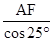 ≈44.4
≈44.4
∴长方形卡片ABCD的周长为(44.4+50)×2=190(mm)
则△ABE和△AFD均为直角三角形
在Rt△ABE中,∠ABE=∠α=25°
sin∠ABE=
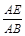 ∴AB=
∴AB=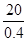 =50
=50 ∵∠FAD=90°-∠BAE,∠α=90°-∠BAE
∴∠FAD=∠α=25°
在Rt△AFD中,cos∠FAD=
AD=
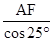 ≈44.4
≈44.4 ∴长方形卡片ABCD的周长为(44.4+50)×2=190(mm)

略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
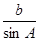
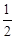 bcsinA.
bcsinA.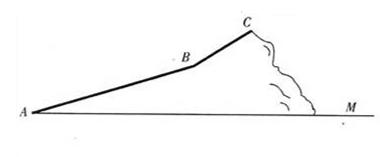
 =________
=________ .
.

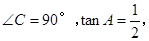
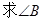 的正弦、余弦值.
的正弦、余弦值.