题目内容
【题目】如图,抛物线y1=ax2+2ax+1与![]() 轴有且仅有一个公共点A,经过点A的直线y2=kx+b交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
轴有且仅有一个公共点A,经过点A的直线y2=kx+b交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
(1)求![]() 的值;
的值;
(2)求直线AB对应的函数解析式;
(3)直接写出当y1 ≥y2 时,![]() 的取值范围.
的取值范围.
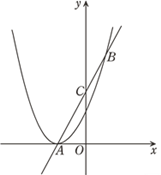
【答案】(1)a的值为1(2)直线AB的解析式为y=2x+2(3)当y1 ≥y2时,x的取值范围为 x≥1或x≤-1
【解析】分析:![]() 根据抛物线
根据抛物线![]() 与
与![]() 轴有且仅有一个公共点,则
轴有且仅有一个公共点,则![]() ,即可求出
,即可求出![]() 的值;
的值;
![]() 求得
求得![]() 的坐标,用待定系数法即可求出直线AB对应的函数解析式;
的坐标,用待定系数法即可求出直线AB对应的函数解析式;
![]() 结合两个函数图象可知当但直线在抛物线上方时可得到
结合两个函数图象可知当但直线在抛物线上方时可得到![]() 的解集.
的解集.
详解:(1)∵抛物线![]() 与x轴有且仅有一个公共点A,
与x轴有且仅有一个公共点A,
∴![]()
解得a1=0(舍去),a2=1,
∴a的值为1.
(2)由(1)得抛物线解析式为![]()
∵![]()
∴顶点A的坐标为![]()
∵点C是线段AB的中点, c的横坐标为0,设B的横坐标为m.
∴![]() ,
,
得m=1.
∴B点的横坐标为1,
∴当x=1时,![]()
∴B(1,4),
把A![]()
![]() 代入
代入![]() 得
得![]() ,
,
解得:![]() ,
,
∴直线AB的解析式为![]()
(3)当 时,x的取值范围为 x≥1或x≤-1.
时,x的取值范围为 x≥1或x≤-1.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某中学举行“校园好声音”歌手大赛,根据初赛成绩,初二和初三各选出5名选手组成初二代表队和初三代表队参加学校决赛。两个队各选出的5名选手的决赛成绩如图所示:
平均数(分) | 中位数(分) | 众数(分) | |
初二 | 85 | ||
初三 | 85 | 100 |
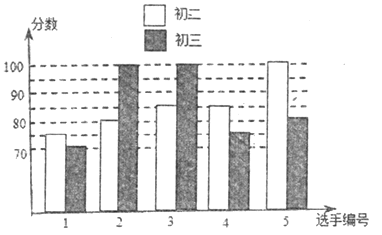
(1)根据图示填写上表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.