题目内容
【题目】过点A0,2的直线l1:y1kxbk0与直线l2:y2x1交于点P2,m。
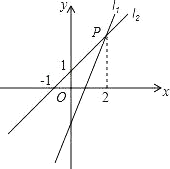
（1）求点P的坐标和直线l1的解析式；
（2）直接写出使得y1y2的x的取值范围。
【答案】(1) y1=
x-2;(2) x≤2．
【解析】
（1）由点P的横坐标利用一次函数图象上点的坐标特征即可求出点P的坐标，根据点A、P的坐标，利用待定系数法即可求出直线l1的解析式；
（2）根据两函数图象的上下位置关系即可得出不等式的解集．
解：（1）当x=2时，m=2+1=3，
∴点P（2，3）．
将点A（0，-2）、P（2，3）代入y1=kx+b中，
得：
，解得：
，
∴直线l1的解析式为y1=x-2．
（2）观察两函数图象可知：
当x＜2时，直线l1在直线l2的下方，
∴使得y1≤y2的x的取值范围为x≤2．
练习册系列答案
相关题目
