��Ŀ����
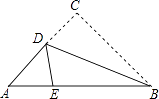
����Ŀ��������ABCD�У���B=60�㣬AB=4������M��ÿ��1����λ���ٶȴӵ�A�����˶�����B����N����ͬ���ٶȴӵ�B�����˶�����C������ͬʱ����������M��MP��AB��ֱ��CD�ڵ�P������NM��NP�����˶�ʱ��Ϊt�룮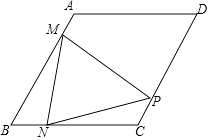
��1����t=2ʱ����NMP=�ȣ�
��2����tΪ��ֵʱ����A��M��C��PΪ������ı�����ƽ���ı��Σ�
��3������NPCΪֱ��������ʱ�����ʱt��ֵ��
���𰸡�
��1��30
��2���⣺����P���߶�CD��ʱ����A��AE��CD��E��
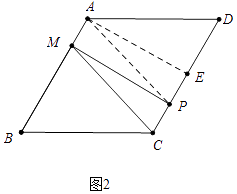
������ABCD�У�AB��CD����D=60�㣬AB=AD=CD=BC=4
��DE= ![]() AD=2��AE=2
AD=2��AE=2 ![]() ��
��
��AM=t��PC=2��t
Ҫʹ�ı���AMCPΪƽ���ı��Σ���AM=PC
��t=2��t��t=1��
����P���߶�DC�ӳ�����ʱ���ı���AMCP����ƽ���ı��Σ�
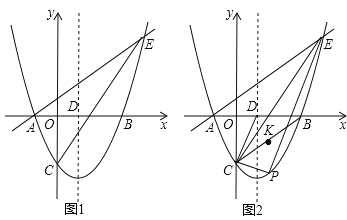
��3���⣺����P���߶�CD��ʱ��������Rt��NPC��
��ֻ�е�P���߶�DC�ӳ�����ʱ���Ŵ���Rt��NPC��
��ͼ3�У�����NPC=90��ʱ����M��N��P��ͬһֱ���ϣ�
���CNP=��MNB=30�㣬
��BM= ![]() BN����4��t=
BN����4��t= ![]() t��
t��
��ã�t= ![]() ��
��
��ͼ4�У�����PNC=90��ʱ��
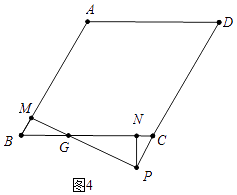
��֪BG=2��4��t����MG= ![]() ��4��t����
��4��t����
GN=t��2��4��t��=3t��8��GP=NG��cos30��= ![]() ��3t��8����
��3t��8����
��PM=2 ![]() ��
��
��MG+GP=2 ![]() ��
��
�� ![]() ��4��t��+
��4��t��+ ![]() ��3t��8��=2
��3t��8��=2 ![]() ��
��
���t=10���������⣬
����������t= ![]() sʱ����PNC��ֱ�������Σ�
sʱ����PNC��ֱ�������Σ�
���������⣺��1����ͼ1�У�����AC��
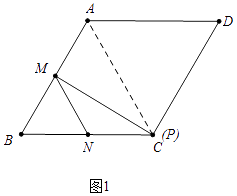
���ı���ABCD�����Σ���B=60�㣬
��AB=BC=CD=AD��
���ABC����ACD���ǵȱ������Σ�
��t=2ʱ��AM=BM=2��BN=CN=2��
��PM��AB��
��PA=PB��
��P��C�غϣ�
��MN��AC��
���NMP=��ACM= ![]() ��ACB=30�㣮
��ACB=30�㣮
��2������P���߶�CD��ʱ����A��AE��CD��E��

������ABCD�У�AB��CD����D=60�㣬AB=AD=CD=BC=4
��DE= ![]() AD=2��AE=2
AD=2��AE=2 ![]() ��
��
��AM=t��PC=2��t
Ҫʹ�ı���AMCPΪƽ���ı��Σ���AM=PC
��t=2��t��t=1��
����P���߶�DC�ӳ�����ʱ���ı���AMCP����ƽ���ı��Σ�
��3������P���߶�CD��ʱ��������Rt��NPC��
��ֻ�е�P���߶�DC�ӳ�����ʱ���Ŵ���Rt��NPC��
��ͼ3�У�����NPC=90��ʱ����M��N��P��ͬһֱ���ϣ�
���CNP=��MNB=30�㣬
��BM= ![]() BN����4��t=
BN����4��t= ![]() t��
t��
��ã�t= ![]() ��
��
��ͼ4�У�����PNC=90��ʱ��

��֪BG=2��4��t����MG= ![]() ��4��t����
��4��t����
GN=t��2��4��t��=3t��8��GP=NG��cos30��= ![]() ��3t��8����
��3t��8����
��PM=2 ![]() ��
��
��MG+GP=2 ![]() ��
��
�� ![]() ��4��t��+
��4��t��+ ![]() ��3t��8��=2
��3t��8��=2 ![]() ��
��
���t=10���������⣬
����������t= ![]() sʱ����PNC��ֱ�������Σ�
sʱ����PNC��ֱ�������Σ�
���Դ��ǣ���1��30����2��t=1����3��t=![]() .
.
�����㾫����ͨ���������ƽ���ı��ε����ʣ�����ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�ּ����Խ����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�