Question

【题目】在平面直角坐标系中，已知抛物线．

（1）抛物线的对称轴为直线________．

（2）当时，函数值的取值范围是，求和的值．

（3）当时，解决下列问题．

①抛物线上一点到轴的距离为6，求点的坐标．

②将该抛物线在间的部分记为，将在直线下方的部分沿翻折，其余部分保持不变，得到的新图象记为，设的最高点、最低点的纵坐标分别为、，若，直接写出的取值范围．

Answer 1

【答案】（1）；（2），；（3）①的坐标为或，②．

【解析】

（1）函数的对称轴为：x=，即可求解；
（2）函数对称轴为x=1，当-2≤x≤2时，函数值y的取值范围是-4≤y≤b，故y=-4是函数的最小值，即抛物线的顶点为（1，-4），即可求解；
（3）①抛物线上一点P到x轴的距离为6，而顶点坐标为（1，-4），故x2-2x-3=6，即可求解；②分M′在点H下方、上方两种情况分别求解即可．

解：（1）函数的对称轴为：x=，
故答案为：x=1；
（2）函数对称轴为x=1，当-2≤x≤2时，函数值y的取值范围是-4≤y≤b，
故y=-4是函数的最小值，即抛物线的顶点为（1，-4），

把代入得，解得

故抛物线的表达式为：y=x2-2x-3，
则b=（-2）2-2（-2）-3=5；

（3）①∵抛物线上一点P到x轴的距离为6，而顶点坐标为（1，-4），
故x2-2x-3=6，解得：x=1±，
故点P的坐标为（1+，6）或（1-，6）；
②设图象折叠后顶点M的对应点为M′，点H是x=4函数所处的位置，图象Q为C′M′NH区域，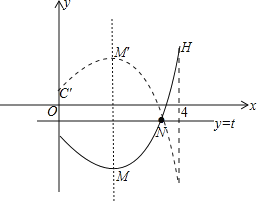

点M（1，-4），点H（4，5），则点M′（1，2t+4），
当点M′在点H下方时，2t+4≤5，t≤，
函数Q的最高点为H，最低点为N，

则5-t≤6，解得：t≥-1，
故-1≤t≤；
当点M′在点H上方时，
同理可得：≤t≤2；

故的取值范围是：-1≤t≤2．