Question

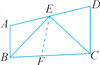
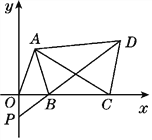
【题目】（1）一条直线可以把平面分成两个部分（或区域），如图，两条直线可以把平面分成几个部分？三条直线可以把平面分成几个部分？试画图说明．

（2）四条直线最多可以把平面分成几个部分？试画出示意图，并说明这四条直线的位置关系．

（3）平面上有条直线，每两条直线都恰好相交，且没有三条直线交于一点，处于这种位置的条直线分一个平面所成的区域最多，记为，试研究与之间的关系．

思维方法天地

Answer 1

【答案】答案见解析

【解析】试题分析：（1）分别得到两条直线平行和相交，三条直线平行和交于一点和两两相交的结果；

（2）只有四条直线两两相交时，才能将平面分得最多，分别画出图形即可求得所分平面的部分；

（3）一条直线可以把平面分成两部分，两条直线最多可以把平面分成4部分，三条直线最多可以把平面分成7部分，四条直线最多可以把平面分成11部分，可以发现，两条直线时多了2部分，三条直线比原来多了3部分，四条直线时比原来多了4部分，…，n条时比原来多了n部分，由此即可得.

试题解析：（1）如图1，两条直线因其位置不同，可以分别把平面分成个或个区域；

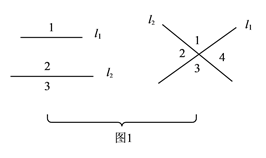
如图2，三条直线因其位置关系的不同，可以分别把平面分成个、个和个区域．

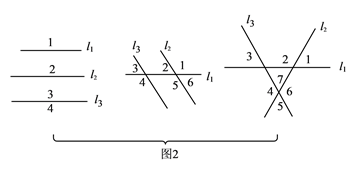
（2）如图3，四条直线最多可以把平面分成个区域，此时这四条直线位置关系是两两都相交，且无三线共点．

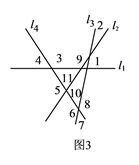
（3）平面上条直线两两相交，且没有三条直线交于一点，把平面分成个区域，平面本身就是一个区域，当时， ；

当时， ；

当时， ；

当时， ，……由此可以归纳公式