题目内容
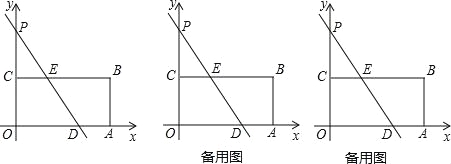
【题目】如图，在四边形ABCD中，AB∥DC，BE，CE分别平分∠ABC，∠BCD，且点E在AD上．求证：BC＝AB＋CD.
【答案】证明见解析
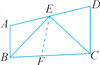
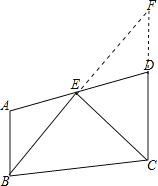
【解析】试题分析：延长BE交CD的延长线于点F，首先证明CF=BC，再根据等腰三角形的性质可得BE=EF，然后证明△ABE≌△FDE，进而得到FD=AB，再利用等量代换可得BC=AB+DC．
试题解析：延长BE交CD的延长线于点F，
∵BE平分∠ABC，
∴∠ABE=∠CBE，
∵AB∥CD，
∴∠F=∠ABE，∠A=∠FDA，
∴∠F=∠CBE，
∴CF=BC，
∵CE平分∠BCD，
∴BE=EF（三线合一）），
在△ABE和△DFE中，
，
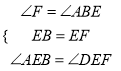∴△ABE≌△FDE（ASA），
∴FD=AB，
∵CF=DF+CD，
∴CF=AB+CD，
∴BC=AB+CD．
练习册系列答案
相关题目
【题目】宏远商贸公司有A、B两种型号的商品需运出，这两种商品的体积和质量分别如下表所示：
体积（m3/件） | 质量（吨/件） | |
A型商品 | 0.8 | 0.5 |
B型商品 | 2 | 1 |
（1）已知一批商品有A、B两种型号，体积一共是20m3，质量一共是10.5吨，求A、B两种型号商品各有几件？
（2）物流公司现有可供使用的货车每辆额定载重3.5吨，容积为6m3，其收费方式有以下两种：
①按车收费：每辆车运输货物到目的地收费600元；
②按吨收费：每吨货物运输到目的地收费200元．
要将（1）中的商品一次或分批运输到目的地，宏远商贸公司应如何选择运送、付费方式运费最少并求出该方式下的运费是多少元？
