题目内容
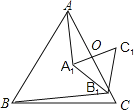
【题目】如图,△ABC和△A1B1C1均为等边三角形,点O既是AC的中点,又是A1C1的中点,则AA1:BB1=_____.
【答案】1∶![]()
【解析】
连接OB,O B1,根据等边三角形的性质求出OB⊥AC,B1O⊥A1 C1,推出∠BO B1=∠CO C1=∠AO A1,求出AB=2AO,A1B1=2 A1O,由勾股定理求出由勾股定理得:OB=![]() AO,O B1=
AO,O B1=![]() A1O,即
A1O,即![]() =
=![]() ,,证△AO A1∽△BO B1,得出比例式,即可得出答案.
,,证△AO A1∽△BO B1,得出比例式,即可得出答案.
解:连接OB,O B1,

∵△ABC和△A1B1C1均为等边三角形,点O既是AC的中点,又是![]() 的中点,
的中点,
∴OB⊥AC,B1O⊥A1 C1,
∴∠BOC=∠C1O B1=90°,
∵∠CO B1=∠CO B1,
∴∠BO B1=∠CO C1=∠AO A1,
AB=2AO,A1B1=2 A1O,
由勾股定理得:OB=![]() AO,O B1=
AO,O B1=![]() A1O,
A1O,
即![]() =
=![]() ,
,
∵∠BO B1=∠CO C1=∠AO A1,
∴△AO A1∽△BO B1,
即AA1:BB1=1:![]() .
.
故答案为:1:![]() .
.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
【题目】下表是小颖往表姐家打长途电话的收费记录:
通话时间x(分钟) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
电话费y(元) | 3 | 3 | 3 | 3.6 | 4.2 | 4.8 | 5.4 |
(1)上表的两个变量中, 是自变量, 是因变量;
(2)写出y与x之间的关系式;
(3)若小颖的通话时间是15分钟,则需要付多少电话费?
(4)若小颖有24元钱,则她最多能打多少分钟电话?