题目内容
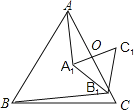
【题目】已知:如图,在△ABC中,AB=AC.
(1)尺规作图:作∠BAC的角平分线AD,交BC于点D.(不要求写作法,保留作图痕迹)
(2)延长AD至E点,使DE=AD,连接BE、CE.求证:四边形ABEC是菱形.
【答案】
(1)解:如图,AD为所求作的∠BAC的平分线

(2)证明:如图,

∵AD平分∠BAC,
∴∠BAD=∠CAD,
又∵AB=AC,
∴BD=CD,
又∵AD=DE,
∴四边形ABEC是平行四边形.
又∵AB=AC,
∴四边形ABEC是菱形.
【解析】(1)根据全等三角形的判定方法作出∠BAC的角平分线AD;(2)根据等腰三角形的性质(三线合一),得到BD=CD,根据对角线互相平分的四边形是平行四边形,得到四边形ABEC是平行四边形,根据菱形的定义得到四边形ABEC是菱形.
【考点精析】本题主要考查了菱形的判定方法的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能正确解答此题.

练习册系列答案
相关题目
【题目】铁一课间餐种类繁多,深受学生喜爱.这天饭堂在课间的出品有鸡腿、薯饼、鱼丸和鸡柳.某同学就九年级学生对课间餐各类食物的喜爱程度做了抽样调查,制成表格如下:
课间餐种类 | 人类 | 百分比 |
鸡腿 | 150 | 60% |
薯饼 | 30 | a |
鱼丸 | b | 12% |
鸡柳 | 40 | c |
(1)样本容量是 , a= , b= , c= .
(2)若小王和小李商议着一起去买课间餐,若他们对以上四种口味的课间餐喜爱程度相同.请你帮他们算一算他们买了相同课间餐的概率.