题目内容
【题目】如图,在平行四边形![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点E,交
于点E,交![]() 的延长线于F,以
的延长线于F,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() 。
。
(1)证明平行四边形![]() 是菱形;
是菱形;
(2)若![]() ,连结
,连结![]() ,①求证:
,①求证:![]() ;②求
;②求![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,
,![]() ,M是
,M是![]() 的中点,求
的中点,求![]() 的长。
的长。

【答案】(1)见解析;(2)①见解析;②∠BDG=60°;(3)![]()
【解析】
(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质和角平分线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再根据四边形ECFG是平行四边形,可得四边形ECFG为菱形;
(2)①根据已知和菱形的性质得出∠BEG=120°=∠DCG,再判断出AB=BE,进而得出BE=CD,即可判断出△BEG≌△DCG(SAS)
②先得出∠CGE=60°再由①得出△BDG是等边三角形,即可得出结论;
(3)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到△BDM是等腰直角三角形,等腰直角三角形的性质即可得到结论.
解:(1)证明:∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)①∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=![]() ∠BCF=60°,
∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△BEG≌△DCG(SAS),
②∵△BEG≌△DCG
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)连接BM,MC,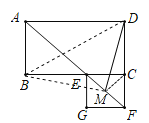
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
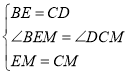
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=8,AD=14,
∴BD=2![]() ,
,
![]()

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案