题目内容
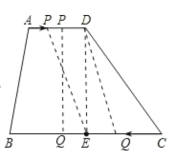
【题目】如图，在四边形ABCD中，AD∥BC，AD＝5，BC＝18，E是BC的中点．点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒3个单位长度的速度从点C出发，沿CB向点B运动．点P停止运动时，点Q也随之停止运动，当运动时间t秒时，以点P，Q，E，D为顶点的四边形是平行四边形，则t的值为_____．
【答案】2秒或3.5秒
【解析】
由AD∥BC，则PD=QE时，以点P，Q，E，D为顶点的四边形是平行四边形，
①当Q运动到E和C之间时，设运动时间为t，则得：9-3t=5-t，解方程即可；
②当Q运动到E和B之间时，设运动时间为t，则得：3t-9=5-t，解方程即可．
∵E是BC的中点，
∴BE=CE=
BC=9，
∵AD∥BC，
∴PD=QE时，以点P，Q，E，D为顶点的四边形是平行四边形，
①当Q运动到E和C之间时，设运动时间为t，
则得：93t=5t，
解得：t=2，
②当Q运动到E和B之间时，设运动时间为t，
则得：3t9=5t，
解得：t=3.5；
∴当运动时间t为2秒或3.5秒时，以点P，Q，E，D为顶点的四边形是平行四边形．
故答案为：2秒或3.5秒．
练习册系列答案
相关题目
