Question

【题目】问题探究

(1)如图1,已知锐角△ABC中,点D在BC边上,当线段AD最短时,请你在图中画出点D的位置.

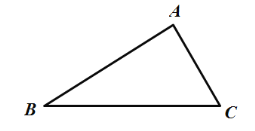
图1

(2)若一个四边形的四个顶点分别在一个三角形的三条边上;则称这个四边形为该三角形的内接四边形.

如图2,在Rt△ABC中,AB=6,BC=8,∠B=90°.矩形BEFG是△ABC的内接矩形,若EF=2,则矩形BEFG的面积为_________

如图3,在△ABC中,AB=,BC=8,∠B=45°,矩形DEFG是△ABC的一个内接矩形且D、E在边BC上.若EF=2,求矩形DEFG的面积;

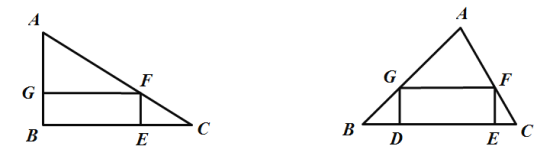
图2 图3

问题解决:

(3)如图4,△ABC是一块三角形木板余料,AB=6,BC=8,∠B=30°,木匠师傅想利用它裁下一块矩形DEFG木块,矩形DEFG是△ABC的一个内接矩形且D、E在边BC上,请在图4中画出对角线DF最短的矩形DEFG,请说明理由,并求出此时DF的长度.

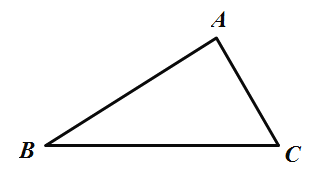
图4

Answer 1

【答案】（1）详见解析；（2）；；（3）.

【解析】

（1）根据点到直线的距离，垂线段最短可得：过点A作AD⊥BC交BC于点D，则线段AD即为所求；

（2）①由矩形性质可得：EF//AB,则△ABC∽△FEC，所以，即，解得EC＝，从而求得BE＝8－＝，从而求得S矩形BEFG的面积；

②过点A作AH⊥BC于点H，由∠B=45°，AB＝可得：BH＝AH＝6，则CH＝BC－BH＝8－6＝2，由矩形性质可得：EF＝DG＝2，EF//AH//DG，则△BDG∽△ABH，△ACH∽FCE，则，从而求得BD＝2，CE＝，从而求得DE＝BC－BD－CE＝8－2－＝，从而求得矩形BEFG的面积；

问题解决:

(3) 过点A作AH⊥BC于点H，由∠B=30°，AB＝可得：AH＝3，BH＝3，则CH＝BC－BH＝8－3，设EF＝x,由矩形性质可得：EF＝DG＝x，EF//AH//DG，则△BDG∽△ABH，△ACH∽FCE，则从而求得BD＝,CE＝，则DF＝BC－BD－CE＝8－，又由DF＝可得，则求DF最小值即转化为求的最小值.

（1）如图所示：过点A作AD⊥BC交BC于点D，则线段AD即为所求；

（2）①∵四边形BEFG是矩形，

∴EF//AB,

∴△ABC∽△FEC，

∴，

又∵EF＝2，AB＝6，BC＝8，

∴，解得EC＝，

又∵BE＝BC－EC，

∴BE＝8－＝，

∴S矩形BEFG＝；

②过点A作AH⊥BC于点H，如图所示：

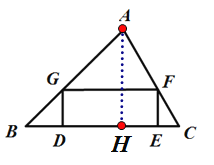
∵∠B=45°，AB＝

∴BH＝AH＝6，

又∵BC＝8，

∴CH＝BC－BH＝8－6＝2，

∵四边形BEFG是矩形，

∴EF＝DG＝2，EF//AH//DG，

∴△BDG∽△ABH，△ACH∽FCE，

∴，

又∵AH＝6，DG＝2，BH＝6，EF＝2，

∴BD＝2，CE＝，

又∵DE＝BC－BD－CE

∴DE＝8－2－＝，

∴矩形BEFG的面积为：;

(3) 过点A作AH⊥BC于点H，如图所示：

∵∠B=30°，AB＝，

∴AH＝3，BH＝3，

又∵BC＝8，

∴CH＝BC－BH＝8－3，

设EF＝x,

四边形BEFG是矩形，

∴EF＝DG＝x，EF//AH//DG，

∴△BDG∽△ABH，△ACH∽FCE，

∴，

即为：

∴BD＝,CE＝，

∴DE＝BC－BD－CE＝8－－=＝8－，

又∵DF＝

∴当x=时，DF有最小值为＝.