题目内容
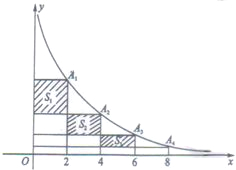 在反比例函数y=
在反比例函数y=| 10 | x |
分析:由已知条件横坐标成等差数列,再根据点A1、A2、A3、…、An、An+1在反比例函数上,求出各点坐标,再由面积公式求出Sn的表达式,把n=1代入求得S1的值.
解答:解:∵点A1、A2、A3、…、An、An+1在反比例函数y=
(x>0)的图象上,且每点的横坐标与它前一个点的横坐标的差都为2,
又点A1的横坐标为2,
∴A1(2,5),A2(4,
)
∴S1=2×(5-
)=5;
由题图象知,An(2n,
),An+1(2n+2,
),
∴S2=2×(
-
)=
,
∴图中阴影部分的面积知:Sn=2×(
-
)=
,(n=1,2,3,…)
∵
=
-
,
∴S1+S2+S3+…+Sn=10(
+
+…+
)=10(1-
+
-
+…
-
)=
.
故答案为:
.
| 10 |
| x |
又点A1的横坐标为2,
∴A1(2,5),A2(4,
| 5 |
| 2 |
∴S1=2×(5-
| 5 |
| 2 |
由题图象知,An(2n,
| 10 |
| 2n |
| 10 |
| 2n+2 |
∴S2=2×(
| 10 |
| 4 |
| 10 |
| 6 |
| 5 |
| 3 |
∴图中阴影部分的面积知:Sn=2×(
| 10 |
| 2n |
| 10 |
| 2n+2 |
| 10 |
| n(n+1) |
∵
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴S1+S2+S3+…+Sn=10(
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 10n |
| n+1 |
故答案为:
| 10n |
| n+1 |
点评:此题是一道规律题,首先根据反比例函数的性质及图象,求出An的坐标的表达式,再由此求出Sn的表达式.

练习册系列答案
相关题目
 如图所示,点P1,P2,P3,…,P10在反比例函数y=
如图所示,点P1,P2,P3,…,P10在反比例函数y=| 6 |
| x |
A、Q10(
| ||
B、Q10(
| ||
C、Q10(
| ||
| D、Q10(19,0) |
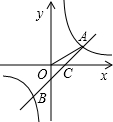
 如图:在平面直角坐标系中,△ABC是等腰直角三角形,∠ACB=Rt∠,CA⊥x轴,垂足为点A.点B在反比例函数
如图:在平面直角坐标系中,△ABC是等腰直角三角形,∠ACB=Rt∠,CA⊥x轴,垂足为点A.点B在反比例函数