题目内容
在反比例函数y=-
(x>0)的图象上有一点A到原点O的距离为
,则A的坐标为
| 3 |
| x |
| 10 |
(1,-3),(3,-1)
(1,-3),(3,-1)
.分析:首先设A(m,-
),根据勾股定理可得m2+(-
)2=10,再解方程可得m的值,进而得到A点坐标.
| 3 |
| m |
| 3 |
| m |
解答:解:设A(m,-
),由题意得:
m2+(-
)2=10,
整理得:m4-10m2+9=0,
解得:m2=1,m2=9,
故m=±1或±3,
A(1,-3),(-1,3),(3,-1),(-3,1).
∵x>0,
∴A(1,-3),(3,-1).
故答案为:(1,-3),(3,-1).
| 3 |
| m |
m2+(-
| 3 |
| m |
整理得:m4-10m2+9=0,
解得:m2=1,m2=9,
故m=±1或±3,
A(1,-3),(-1,3),(3,-1),(-3,1).
∵x>0,
∴A(1,-3),(3,-1).
故答案为:(1,-3),(3,-1).
点评:此题主要考查了反比例函数图象上点的坐标特点,关键是掌握勾股定理,求出m的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
点(1,2)在反比例函数y=
的图象上,则k的值是( )
| 1-k |
| x |
| A、0 | B、1 | C、-1 | D、-2 |
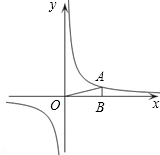 如图,在直角坐标系中,O为坐标原点.已知反比例函数y=
如图,在直角坐标系中,O为坐标原点.已知反比例函数y=