题目内容
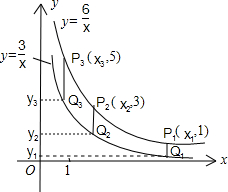
 如图所示,点P1,P2,P3,…,P10在反比例函数y=
如图所示,点P1,P2,P3,…,P10在反比例函数y=| 6 |
| x |
A、Q10(
| ||
B、Q10(
| ||
C、Q10(
| ||
| D、Q10(19,0) |
分析:根据已知条件“纵坐标分别为1,3,5,…,等10个连续的奇数”总结出规律Pn(x,2n-1)(n∈N+),然后由反比例函数图象上的点的坐标特征,将Pn代入反比例函数的解析式y=
,从而求得Qn的横坐标xn的值.
| 6 |
| x |
解答:解:∵点P1,P2,P3,…,P10在反比例函数y=
的第一象限内的图象上,它们的纵坐标分别为1,3,5,…,等10个连续的奇数,
∴Pn(xn,2n-1)(n∈N+),
∴P10(x10,19)(n∈N+);
∴19=
,
解得,x10=
;
∴Q10(
,0).
故选B.
| 6 |
| x |
∴Pn(xn,2n-1)(n∈N+),
∴P10(x10,19)(n∈N+);
∴19=
| 6 |
| x10 |
解得,x10=
| 6 |
| 19 |
∴Q10(
| 6 |
| 19 |
故选B.
点评:本题主要考查了反比例函数上点的坐标特征(经过函数的某点一定在函数的图象上).解答此题的难点是根据P点的“纵坐标分别为1,3,5,…,等10个连续的奇数”找出Pn的坐标的规律Pn(x,2n-1)(n∈N+),然后再根据反比例函数图象上的点的坐标特征求得Qn的横坐标xn的值.

练习册系列答案
相关题目
 两个反比例函数y=
两个反比例函数y= 两个反比例函数y=
两个反比例函数y= 两个反比例函数
两个反比例函数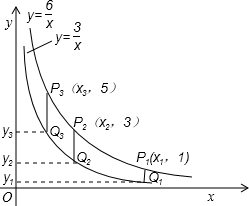 两个反比例函数y=
两个反比例函数y=