题目内容
【题目】在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.已知抛物线y=-![]() 与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______.
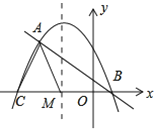
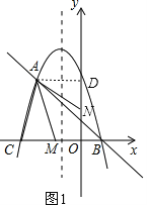
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点M的坐标.
【答案】(1)y=-![]() x+
x+![]() ;(-2,2
;(-2,2![]() );(1,0);(2)N点坐标为(0,2
);(1,0);(2)N点坐标为(0,2![]() -3)或(
-3)或(![]() ,
,![]() )
)
【解析】
(1)由“梦想直线”的定义可求得其解析式,联立直线与抛物线的解析式可求得A,B的坐标;
(2)根据“梦想三角形”的定义,分当点N在y轴上时和当M点在y轴上时两种情况讨论即可.
解(1)由“梦想直线”的定义得,抛物线的“梦想直线”的解析式为y=-![]() x+
x+![]() ,
,
联立梦想直线与抛物线解析式可得 ,解得
,解得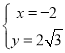 或
或![]() ,
,
∴A(-2,2![]() ),B(1,0),
),B(1,0),
故答案为:y=-![]() x+
x+![]() ;(-2,2
;(-2,2![]() );(1,0);
);(1,0);
(2)当点N在y轴上时,△AMN为梦想三角形,
如图1,过A作AD⊥y轴于点D,则AD=2,
在y=-![]() x2-
x2-![]() x+2
x+2![]() 中,令y=0可求得x=-3或x=1,
中,令y=0可求得x=-3或x=1,
∴C(-3,0),且A(-2,2![]() ),
),
∴AC=![]() =
=![]() ,
,
由翻折的性质可知AN=AC=![]() ,
,
在Rt△AND中,由勾股定理可得DN=![]() =3,
=3,
∵OD=2![]() ,
,
∴ON=2![]() -3或ON=2
-3或ON=2![]() +3,
+3,
当ON=2![]() +3时,则MN>OD>CM,与MN=CM矛盾,不合题意,
+3时,则MN>OD>CM,与MN=CM矛盾,不合题意,
∴N点坐标为(0,2![]() -3);
-3);
当M点在y轴上时,则M与O重合,过N作NP⊥x轴于点P,如图2,

在Rt△AMD中,AD=2,OD=2![]() ,
,
∴tan∠DAM=![]() =
=![]() ,
,
∴∠DAM=60°,
∵AD∥x轴,
∴∠AMC=∠DAO=60°,
又由折叠可知∠NMA=∠AMC=60°,
∴∠NMP=60°,且MN=CM=3,
∴MP=![]() MN=
MN=![]() ,NP=
,NP=![]() MN=
MN=![]() ,
,
∴此时N点坐标为(![]() ,
,![]() );
);
综上可知N点坐标为(0,2![]() -3)或(
-3)或(![]() ,
,![]() );
);

 优生乐园系列答案
优生乐园系列答案