题目内容
【题目】如图,在△ABC中,∠ACB=90°,CA=CB,点O在△ABC的内部,⊙O经过B,C两点,交AB于点D,连接CO并延长交AB于点G,以GD,GC为邻边作GDEC.
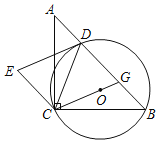
(1)判断DE与⊙O的位置关系,并说明理由.
(2)若点B是![]() 的中点,⊙O的半径为2,求
的中点,⊙O的半径为2,求![]() 的长.
的长.
【答案】(1)DE是⊙O的切线,理由见解析;(2)![]() π
π
【解析】
(1) 连接OD,由题意可得∠ABC=45°,再结合圆周角定理可得∠COD=2∠ABC=90°,再由平行四边形GDEC可得,∠EDO+∠COD=180°,即∠EDO=90°,即可完成证明;
(2) 连接OB,可得点B是![]() 的中点,进一步说明∠BOC=∠BOD,在确定∠BOC的度数,最后用弧长公式求解即可·
的中点,进一步说明∠BOC=∠BOD,在确定∠BOC的度数,最后用弧长公式求解即可·
解:(1)DE是⊙O的切线;理由如下:
连接OD,
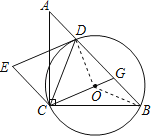
∵∠ACB=90°,CA=CB,
∴∠ABC=45°,
∴∠COD=2∠ABC=90°,
∵四边形GDEC是平行四边形,
∴DE∥CG,
∴∠EDO+∠COD=180°,
∴∠EDO=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)连接OB,

∵点B是![]() 的中点,
的中点,
∴![]() ,
,
∴∠BOC=∠BOD,
∵∠BOC+∠BOD+∠COD=360°,
∴∠BOC=![]() =135°
=135°
∴![]() 的长=
的长=![]() =
=![]() π.
π.

练习册系列答案
相关题目
【题目】某商店销售一种商品,经市场调査发现,该商品的周销售量y(件)是售价x(元/件)的一次函数.其售价、周销售量、周销售利润w(元)的三组对应值如表:
售价x(元/件) | 50 | 60 | 80 |
周销售量y(件) | 100 | 80 | 40 |
周销售利润w(元) | 1000 | 1600 | 1600 |
注:周销售利润=周销售量×(售价﹣进价)
(1)求y关于x的函数解析式_____;
(2)当售价是_____元/件时,周销售利润最大.