题目内容
| |||||||||
答案：
解析：
解析：
(1) |
过D作DG⊥AB于G，在直角梯形ABCD中，∠DCB=∠CBA=90°．在直角梯形ABCD中，∠DCB=∠CBA=90°．∵∠DGB=90°，∴四边形DGBC是矩形，∴DC=BG．∵AB=2CD，∴AG=GB，∴DA=DB，∵∠DAB=∠DBA．又∵EF∥AB，AE与BF相交于D点，∴四边形ABFE是等腰梯形． |
(2) |
∵CD∥AB，∴ |
．∵AB=2CD，∴AF=2CF．∵CF=4，∴AF=8．∵∠CBA=90°，AC⊥BF，∴Rt△BCF∽Rt△ABF．∴
，∴
．∴
．∵四边形ABFE是等腰梯形，∴
．
练习册系列答案
相关题目
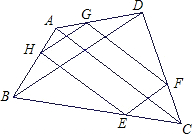在四边形ABCD中，AC、BD是四边形ABCD的两条对角线，点E、F、G、H分别是在四边形ABCD的四边上的动点，但E、F、G、H不与A、B、C、D重合，且EF∥BD∥GH，FG∥AC∥HE．
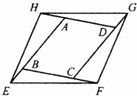21、如图，分别延长?ABCD的四边，使BE=CF=DG=AH．
如图，过平行四边形ABCD对角线的交点O作两条互相垂直的直线EF、GH分别交平行四边形ABCD四边于E、G、F、H，求证：四边形EGFH是菱形．