题目内容
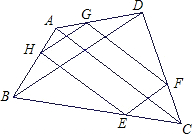 在四边形ABCD中,AC、BD是四边形ABCD的两条对角线,点E、F、G、H分别是在四边形ABCD的四边上的动点,但E、F、G、H不与A、B、C、D重合,且EF∥BD∥GH,FG∥AC∥HE.
在四边形ABCD中,AC、BD是四边形ABCD的两条对角线,点E、F、G、H分别是在四边形ABCD的四边上的动点,但E、F、G、H不与A、B、C、D重合,且EF∥BD∥GH,FG∥AC∥HE.(1)若对角线AC=BD=a(定值),求证:四边形EFGH的周长是定值;
(2)若AC=m,BD=n,m、n为定值,但m≠n,则四边形EFGH的周长是定值吗?请指出,并说明理由.
分析:(1)首先EF∥BD∥GH,FG∥AC∥HE可以证明四边形EFGH为平行四边形,设GH为x,GF为y,AH=p,BH=q,然后利用平行线分线段成比例可以得到即
=
,
=
,即
=
,
=
,然后即可求出x+y,也就求出了四边形EFGH的周长,最后就证明了四边形EFGH的周长是定值;
(2)利用(1)中的结论,根据AC=m,BD=n,求出x+y,然后利用图形的性质讨论即可得到结论.
| AH |
| AB |
| GH |
| BD |
| BH |
| AB |
| HE |
| AC |
| q |
| p+q |
| y |
| a |
| p |
| p+q |
| x |
| a |
(2)利用(1)中的结论,根据AC=m,BD=n,求出x+y,然后利用图形的性质讨论即可得到结论.
解答:解:(1)∵EF∥BD∥GH,FG∥AC∥HE
∴四边形EFGH是平行四边形,
设GH为x,GF为y,AH=p,BH=q
∵GH∥BD,BD=a
∴
=
,
即
=
,
∵HE∥AC,AC=a
∴
=
,
即
=
,
∴x+y=
=a,
故四边形EFGH的周长=2(x+y)=2a;
(2)∵AC=m,BD=n,
则有
=
,
=
,
∴x+y=
=
,
∵m、n为确定的值,H是AB上的动点,
是变量,
而x+y随
的变化而变化,
∴x+y不能确定,即四边形EFGH的周长不是定值.

∴四边形EFGH是平行四边形,
设GH为x,GF为y,AH=p,BH=q
∵GH∥BD,BD=a
∴
| AH |
| AB |
| GH |
| BD |
即
| p |
| p+q |
| x |
| a |
∵HE∥AC,AC=a
∴
| BH |
| AB |
| HE |
| AC |
即
| q |
| p+q |
| y |
| a |
∴x+y=
| a(p+q) |
| p+q |
故四边形EFGH的周长=2(x+y)=2a;
(2)∵AC=m,BD=n,
则有
| y |
| m |
| p |
| p+q |
| x |
| n |
| q |
| p+q |
∴x+y=
| pm+qn |
| p+q |
| ||
|
∵m、n为确定的值,H是AB上的动点,
| p |
| q |
而x+y随
| p |
| q |
∴x+y不能确定,即四边形EFGH的周长不是定值.
点评:此题比较复杂,要分类讨论,主要考查平行线分线段成比例定理,有的同学因为没有找准对应关系,从而导致错误答案.

练习册系列答案
相关题目
 11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
11、如图所示,在四边形ABCD中,BD是它的一条对角线,若∠1=∠2,∠A=55°16′,则∠ADC=
 如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?
如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是边DC的中点,N是边AB的中点.△MPN是什么三角形?为什么?