题目内容
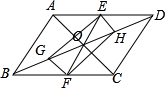
 如图,过平行四边形ABCD对角线的交点O作两条互相垂直的直线EF、GH分别交平行四边形ABCD四边于E、G、F、H,求证:四边形EGFH是菱形.
如图,过平行四边形ABCD对角线的交点O作两条互相垂直的直线EF、GH分别交平行四边形ABCD四边于E、G、F、H,求证:四边形EGFH是菱形.分析:根据对角线互相垂直的平行四边形是菱形.由已知条件证明OH=OG,同理OE=OF,所以四边形EFGH是平行四边形,又因为EF⊥GH,所以四边形EGFH是菱形.
解答: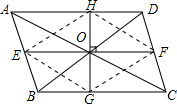 证明:如图,顺次连接点E、G、F、H.
证明:如图,顺次连接点E、G、F、H.
在平行四边形ABCD中,OD=OB,OA=OC,AD∥CB,
∴∠OBG=∠HDO.
∴在△OBG与△ODE中,
,
∴△OBG≌△ODE(ASA),
∴OH=OG.
同理OE=OF,
∴四边形EFH是平行四边形,
又∵EF⊥HG,
∴平行四边形EGFH是菱形.
 证明:如图,顺次连接点E、G、F、H.
证明:如图,顺次连接点E、G、F、H.在平行四边形ABCD中,OD=OB,OA=OC,AD∥CB,
∴∠OBG=∠HDO.
∴在△OBG与△ODE中,
|
∴△OBG≌△ODE(ASA),
∴OH=OG.
同理OE=OF,
∴四边形EFH是平行四边形,
又∵EF⊥HG,
∴平行四边形EGFH是菱形.
点评:此题主要考查菱形的判定,综合利用平行四边形的判定.

练习册系列答案
相关题目
 20、已知:如图,过平行四边形ABCD的对角线交点O作互相垂直的两条直线EG、FH与平行四边形ABCD各边分别相交于点E、F、G、H.求证:四边形EFGH是菱形.
20、已知:如图,过平行四边形ABCD的对角线交点O作互相垂直的两条直线EG、FH与平行四边形ABCD各边分别相交于点E、F、G、H.求证:四边形EFGH是菱形. 10、如图,过平行四边形ABCD的顶点A分别引高AE、AF,如果AE=3.5,AF=2.8,∠EAF=30°,则AB=
10、如图,过平行四边形ABCD的顶点A分别引高AE、AF,如果AE=3.5,AF=2.8,∠EAF=30°,则AB= 23、已知:如图,过平行四边形ABCD的对角线AC的中点O作一条直线,分别交AD、BC于点E、F.
23、已知:如图,过平行四边形ABCD的对角线AC的中点O作一条直线,分别交AD、BC于点E、F.
 如图,过平行四边形ABCD的对角线的交点O作直线EF交AD、BC分别于E、F,又H、G分别为OB、OD的中点,试问:四边形EHFG为平行四边形吗?为什么?
如图,过平行四边形ABCD的对角线的交点O作直线EF交AD、BC分别于E、F,又H、G分别为OB、OD的中点,试问:四边形EHFG为平行四边形吗?为什么?