题目内容
【题目】如图,A、B是反比例函数y=![]() 上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=
上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=![]() OC,S四边形ABDC=14,则k= .
OC,S四边形ABDC=14,则k= .

【答案】16.
【解析】
试题分析:利用已知条件判断点A与点B的纵横坐标正好相反,从而设出点A的坐标,进而求得点B的坐标,利用SACDB=S△CED-S△AEB,求得点A的坐标后,用待定系数法确定出k的值.
试题解析:如图,分别延长CA,DB交于点E,根据AC⊥y轴于C,BD⊥x轴于D,AC=BD=![]() OC,
OC,
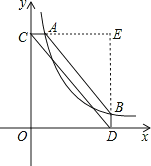
知△CED为直角三角形,且点A与点B的纵横坐标正好相反,
设点A的坐标为(xA,yA),则点B的坐标为(yA,xA),点E的坐标为(yA,yA),
四边形ACDB的面积为△CED的面积减去△AEB的面积.
CE=ED=yA,AE=BE=y-![]() yA,
yA,
∴SACDB=S△CED-S△AEB=![]() [yAyA-(yA-
[yAyA-(yA-![]() yA)(yA-
yA)(yA-![]() yA)]=
yA)]=![]() yA2=14,
yA2=14,
∵yA>0,∴yA=8,
点A的坐标为(2,8),
∴k=2×8=16.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目