题目内容
直角三角形的三边长分别是5,12,13,若此三角形内一点到三边的距离均为x,则x=分析:首先画出草图.根据直角三角形面积计算:两直角边的乘积除以2.另一种计算方法,三个三角形面积的和,并且用三边长与x表示.利用两种方式的计算面积相等,即可求出x的值.
解答: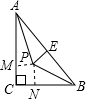 解:S△ABC=
解:S△ABC=
AC•BC=
×5×12
S△ABC=S△ABP+S△APC+S△BPC=
AB•PE+
AC•PM+
BC•PN=
•13x+
•5x+
•12x
∴
×5×12=
•13x+
•5x+
•12x,
即x=2.
故答案为:2.
 解:S△ABC=
解:S△ABC=| 1 |
| 2 |
| 1 |
| 2 |
S△ABC=S△ABP+S△APC+S△BPC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即x=2.
故答案为:2.
点评:本题考查三角形内切圆与圆心.解决本题的关键是通过三角形从不同角度求面积相等,建立关系式,求得x的值.

练习册系列答案
相关题目
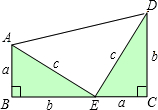 (1)求所拼成的梯形的面积;
(1)求所拼成的梯形的面积;