题目内容
如图所示,是两个相同的直角三角形拼成的梯形ABCD,直角三角形的三边长分别是a、b、c.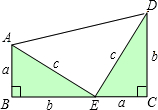 (1)求所拼成的梯形的面积;
(1)求所拼成的梯形的面积;(2)换一种思路求梯形的面积,并说明a、b、c存在数量关系:a2+b2=c2.
分析:(1)根据梯形的面积公式可直接求出面积;
(2)利用△ABE≌△ECD,可得∠AEB=∠EDC,等量代换易求∠AEB+∠EDC=90°,从而可求∠AED是直角,于是可知梯形的面积等于3个直角三角形的面积和,(1)、(2)联合,可证a2+b2=c2.
(2)利用△ABE≌△ECD,可得∠AEB=∠EDC,等量代换易求∠AEB+∠EDC=90°,从而可求∠AED是直角,于是可知梯形的面积等于3个直角三角形的面积和,(1)、(2)联合,可证a2+b2=c2.
解答:解:(1)根据梯形面积公式可知:
S梯形ABCD=
(a+b)×(a+b),
=
(a2+2ab+b2),
=
a2+ab+
b2;
(2)∵△ABE≌△ECD,
∴∠AEB=∠EDC,
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠EDC=90°,
∴∠AED=180°-90°-90°,
∴S梯形ABCD=S△ABE+S△ADE+S△DEC=
ab+
c2+
ab=ab+
c2,
∴
a2+ab+
b2=ab+
c2,
∴a2+b2=c2.
S梯形ABCD=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵△ABE≌△ECD,
∴∠AEB=∠EDC,
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠EDC=90°,
∴∠AED=180°-90°-90°,
∴S梯形ABCD=S△ABE+S△ADE+S△DEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a2+b2=c2.
点评:本题考查了三角形、梯形的面积公式、勾股定理的证明、全等三角形的性质.解题的关键是证明∠AED=90°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
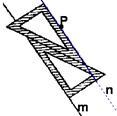 11、如图所示,用两个相同的三角形按照如图方式作平行线,能解释其中道理的定理是
11、如图所示,用两个相同的三角形按照如图方式作平行线,能解释其中道理的定理是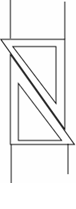
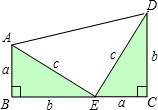 (1)求所拼成的梯形的面积;
(1)求所拼成的梯形的面积;